Por qué Huygens no entendió el analysis situs de Leibniz*
Why Huygens did not understand Leibniz’s analysis situs
Resumen. En 1679 Leibniz envía a Huygens un proyecto de nueva geometría, denominada analysis situs, mediante la cual pretende superar la geometría euclídea. Huygens, sin embargo, en carta a Leibniz afirma que no comprende la utilidad de este nuevo método, ante lo cual Leibniz deja de desarrollarlo. Habitualmente la literatura científica ha incidido en la incomprensión de Huygens por ser una figura centrada en resultados claros y no dado a especulaciones. Sin embargo, si atendemos a estas cartas y al contexto que las rodea, podemos comprobar que la forma en la que Leibniz presentó esta nueva geometría a Huygens pudo impedir que éste la comprendiese adecuadamente.
Palabras clave: Analysis situs, Leibniz, Huygens, Historia de la ciencia, Historia de la filosofía.
Abstract. In 1679 Leibniz sent Huygens a project for a new geometry, called analysis situs, by which he intended to overcome Euclidean geometry. However, Huygens in a letter to Leibniz indicated that he did not understand the usefulness of this new method. Usually, the scientific literature has explained that the reason of this was Huygens’ scientific approach. However, if we look at these letters and their context, we can see that the way in which Leibniz presented this new geometry to Huygens could have prevented him from understanding it properly.
Keywords: Analysis situs, Leibniz, Huygens, History of Science, History of Philosophy.
Recibido: 28/02/2021. Aceptado: 02/03/2021.
* La publicación es parte del proyecto TED2021-130322B-I00, financiado por MCIN/AEI/10.13039/501100011033 y por la Unión Europea “NextGenerationEU”/PRTR.
** Doctor por la Universidad de Sevilla, actualmente es Profesor Ayudante Doctor en el departamento de Lógica y Filosofía Teórica, Universidad Complutense de Madrid. Anteriormente ha sido Visiting Scholar en Harvard University, Investigador Postdoctoral en el CNRS/Aix-Marseille Université, Visiting Researcher en el Leibniz-Archiv de Hannover y Profesor Sustituto Interino en las universidades de Sevilla y de Huelva. Su investigación se centra en la Historia de la Filosofía y de la Ciencia, especialmente en la modernidad temprana, así como en temas relativos a desinformación, fake news y negacionismo. Contacto: mipalomo@ucm.es. Publicaciones recientes: (2021) “New Insight into the Origins of the Calculus War”, Annals of Science 78:1, 22-40; (2020) “El drole de pensée de Leibniz y su ideal de la comunicación científica y filosófica”, Endoxa 46, 441-458.
1. Introducción
Uno de los empeños de Leibniz a lo largo de toda su carrera fue mejorar los métodos generales que figuras científicas tanto antiguas como modernas habían presentado a lo largo de la historia en matemáticas y en geometría. En ese sentido, Euclides y Descartes son dos figuras cuyos métodos Leibniz deseaba superar, buscando los métodos más cómodos y sencillos para aliviar la mente y facilitar la práctica científica. Para conseguirlo, uno de los proyectos más relevantes desarrollados por Leibniz es el analysis situs (AS de ahora en adelante). Si bien mediante la matemática se pueden representar y aprehender fenómenos físicos mediante el uso de magnitudes, ésta no hace referencia al espacio en sí, por lo que los métodos puramente matemáticos darían una solución parcial al problema de cómo representar dichos fenómenos en su totalidad. Por ello, en su época de juventud Leibniz comienza un estudio del situs (espacio) que se una al estudio de las magnitudes presentado por la aritmética para así formular una nueva geometría, la cual permitirá el posterior desarrollo de una teoría fenomenológica del espacio (Arthur, 2013, 526).
Leibniz denomina a este estudio con diferentes términos, entre los que se encuentran AS, característica geométrica, geometría situs, característica situs, análisis geométrico o speciosa situs (Echeverría, 1995, 7). En este trabajo utilizaremos el término AS, siguiendo el consenso que diferentes investigadores han alcanzado a la hora de estudiar el proyecto realizado por Leibniz.
Para comenzar, hay que señalar que Leibniz no publicó en vida nada referente a este AS. Lo más cercano a ello que hizo Leibniz fue enviar a su maestro Christiaan Huygens un extracto de este proyecto en la correspondencia que mantuvieron durante 23 años. Huygens, sin embargo, no llegó a comprender la finalidad ni la utilidad de este análisis de la situación, por lo que a pesar de que el intercambio epistolar se mantuvo en el tiempo hasta 1695 (fecha de fallecimiento de Huygens), nunca volvieron a discutir este método. Ello contrasta con el cálculo infinitesimal de Leibniz: de nuevo, un método creado para “aliviar la mente” a la hora de realizar operaciones matemáticas que es incomprendido por Huygens. Si bien vemos similitudes en la recepción del AS y del cálculo infinitesimal por parte de Huygens, es necesario señalar que, ante la evidencia de la utilidad del cálculo, Huygens sí llegó a reconocer esta utilidad y expresó su deseo de estudiarlo (AA III, 5, 196-202), lo cual nunca llegó a ocurrir con el AS.
La literatura científica, al tratar la incomprensión de Huygens del AS y del cálculo infinitesimal, ha insistido en que Huygens era un cartesiano todavía anclado en métodos clásicos, en comparación con el joven Leibniz y sus seguidores, más inclinados a crear nuevas formas de enfrentarse a los problemas geométricos y matemáticos. Sin embargo, en este trabajo nos gustaría poner en duda que la responsabilidad de la incomprensión del AS sea exclusiva de Huygens, hecho al que apenas se le ha prestado atención en la literatura especializada. Se debe aclarar, sin embargo, que el objetivo primordial de la mayoría de la bibliografía centrada en el AS no se ha enfocado en su recepción por parte de Huygens, lo que exculpa en su gran mayoría a los autores de estar cometiendo un error directo. Más bien, la mayoría de la literatura resalta la incomprensión de Huygens como una forma de contextualizar el AS, y para ello se han valido de lo que podríamos denominar la interpretación tradicional respecto a la recepción del AS de Huygens. Por ejemplo, De Mora, en su magnífica edición de una serie de traducciones de algunos de los tratados matemáticos más importantes de Leibniz, señala que Huygens no entendió en AS por ser un método “muy adelantado a su tiempo” (De Mora, 2018, 107); Freudenthal, en su contextualización histórica del AS, señala que Huygens no disfrutaba tanto de las matemáticas en sí como de sus resultados, lo que podría explicar, junto con la idea de que fue un hombre con una actitud “práctica y sobria”, que no comprendiese el nuevo método leibniziano (Freudenthal, 1972, 63); del mismo modo ocurre con otros textos que se han centrado en presentar una semblanza del AS, su contexto histórico y utilidad: tal es el caso de König, quien en 1752 señaló que Huygens no vio atractivo en las ideas de Leibniz por encontrarse “rempli de ses propres méditations” (König, 1752, 88), posiblemente afianzando la interpretación tradicional respecto a la recepción del AS. Aunque según la hipótesis que mantenemos en este trabajo, la idea de König es incorrecta, hay que destacar que muy probablemente carecía de acceso a la totalidad de la correspondencia entre ellos y a las herramientas críticas que nos ofrece hoy la edición de las obras completas de Leibniz (AA). Vemos, por tanto, que la interpretación tradicional de la recepción del AS es muy temprana en el tiempo.
El hecho de que esta visión de Huygens fuese acogida tan pronto por los investigadores ha facilitado que se haya transmitido a estudios más recientes que retoman dicha interpretación (Huber, 1951, 1999-200; Couturat, 1969, 392; Leibniz, 1968; citados por Echeverría, 1979, 239). También encontramos esta interpretación tradicional en obras publicadas en los últimos años. Por ejemplo, De Risi incide en la pobre recepción del AS por parte de Huygens (De Risi, 2018, 247; 2011, 208), si bien su texto está centrado en los contenidos del AS y no en su contexto histórico; Antognazza señala que Huygens no pudo apreciar el enorme potencial de esta nueva geometría (Antognazza, 2009, 247): aunque su trabajo se trata de una magnífica biografía de referencia en estudios leibnizianos, no realiza un análisis exhaustivo de la recepción del AS, tal y como es de esperar en un trabajo biográfico; Tho señala que Huygens había desalentado de tal manera a Leibniz que el hiato en el proyecto del AS era inevitable (Tho, 2017, 125); por último, en un trabajo escrito en conjunto por Echeverría y De Mora, ambos señalan que Huygens no fue el “interlocutor ideal para este tipo de planteamientos de fundamentación lógica de la geometría”, aunque excusan al científico holandés al estar Leibniz presentando un método que adelantaba “un par de siglos las investigaciones sobre los fundamentos de la geometría” (Echeverría y De Mora, 2016, 113).
Sin embargo, el trabajo realizado por investigadores como Echeverría ha puesto en cuestión dicha interpretación tradicional, pues reconoce que en la fecha de envío del método a Huygens “nadie estaba en condiciones de entender mínimamente la pretensión misma de la geometría leibniciana” (Echeverría, 1984, 77), así como que las ventajas del AS en la carta que Leibniz envía a Huygens son presentadas de un modo confuso (Echeverría, 1979, 234). A pesar de ello, en Echeverría aparecen ecos de la interpretación tradicional, al señalar que Huygens “no se interesó lo más mínimo en el ensayo geométrico que le envió Leibniz” (Echeverría, 1984, 77). Por su parte, Martin ha señalado que, en su carta a Huygens, Leibniz omite algunas reglas que permiten comprender la utilización de los caracteres en el AS, lo que podría ser “una de las razones por la que Huygens no se entusiasmó con la propuesta de Leibniz” (Martin, 1983, 67), junto con el hecho de que este método no fue lo suficientemente desarrollado en su presentación a Huygens (Martin, 1983, 91). Vemos, por tanto, que a pesar de la supervivencia de esta interpretación tradicional, Echeverría y Martin parecen haber sido los únicos que han dado indicios de que el problema de la comprensión del AS no se debe exclusivamente a Huygens, sino que también se debe a la forma en la que Leibniz presenta su método. Esto, sin embargo, no es explicado con detalle en sus trabajos, por lo que investigar esta cuestión es todavía una tarea por realizar.
Es por ello que en este trabajo proponemos la hipótesis de que el motivo de la falta de comprensión de la utilidad del AS por parte de Huygens no se encuentra en su acercamiento al método, sino en la forma en la que Leibniz presenta este proyecto en sus cartas a Huygens, lo cual no ha sido suficientemente tenido en consideración en la literatura especializada. Para ello, tras esta introducción (1), en (2) explicamos los orígenes y primeros desarrollos del AS, de modo que podamos comprender su progreso anterior al envío a Huygens; en (3) tratamos la forma en la que Leibniz introduce a Huygens su nueva geometría; en (4) explicamos las cartas posteriores a la presentación del AS a Huygens y los motivos por los que éste etiquetó al proyecto de Leibniz como “bellos deseos”; en (5) señalamos la posibilidad de que dos textos escritos en 1680 pudiesen haber sido redactados con la finalidad de responder a la opinión negativa de Huygens; para terminar en (6) con nuestras conclusiones.
2. Características y orígenes del analysis situs
El AS es un método formal que mediante símbolos pretende expresar relaciones de espacio, es decir, de posición de objetos o cuerpos. De este modo, mediante el AS se puede expresar cualquier figura o característica geométrica (un círculo, un rectángulo, una recta, un punto). Para Leibniz, la geometría euclídea no ofrece las verdades que están en relación con el mundo fenoménico y que muestran el funcionamiento y forma de relación entre cuerpos, sino que se refieren a un plano geométrico ideal. En contraposición a Euclides, una de las finalidades del AS es conocer las relaciones entre los objetos geométricos, lo cual supone conocer el mundo fenoménico. En consecuencia, las relaciones entre objetos mostrarían, al modo de una analogía, cómo deben ser las relaciones monádicas1 (hasta tal punto que el AS influenció el posterior desarrollo de la monadología: Martin, 1983, 286).
El texto sobre el AS que Leibniz da a conocer a Huygens puede entenderse como el fundamento de sus textos metafísicos de madurez referidos a su teoría del espacio, tal y como defiende Martin (1983, 30-31), idea propuesta también por De Risi (2011, 212, 216; 2007). Este texto se divide en dos: primeramente la carta número 12 de su correspondencia (AA III, 2, n.347: 840-850), y segundo, un artículo adjunto a dicha carta enfocado exclusivamente en el AS (AA III, 2, n.347, 851-860), ambos enviados por Leibniz el 8/18 de septiembre de 1679. Pero es durante el año 1679 cuando Leibniz afianza los conceptos fundamentales de esta nueva geometría que se utilizan en dicho texto, como son el de situs, via, tractus y congruencia. Partiendo de estos conceptos, llega a caracterizar algunas nociones euclidianas y a probar algunos teoremas simples “sin haber recurrido a las figuras ni a las nociones, sino solamente a los nuevos caracteres” (Echeverría, 1995, 20), tarea que le permitirá formular posteriormente su teoría del espacio2.
Para comprender el significado y el contexto que rodea esta carta número 12 debemos retrotraernos a la aparición de algunos de los conceptos claves del AS. Por ejemplo: sabemos que Leibniz escribió una carta no enviada a Gallois que ya nombra la similitud (De Risi, 2007, 58), si bien posteriormente le nombra el proyecto en otra epístola (Antognazza, 2009, 246); también nombra la característica geométrica a Berret; y, por último, describe la posibilidad de un álgebra de situaciones en lugar de magnitudes a Tschirnhaus, quien afirmó que se trataba de una insustancial quimera (De Risi, 2007, 62), algo que evoca la respuesta que Huygens le dará tras recibir este nuevo método. Tal y como podemos comprobar, el AS no fue comprendido por sus contemporáneos. El hecho de que no sólo Huygens, sino tampoco Tschirnhaus entendiese esta nueva geometría, es un fuerte indicio de que el problema no se encuentra en la recepción de Huygens, sino en la forma en la que Leibniz comunica su nuevo método.
Los trabajos iniciales sobre el AS aparecen en su etapa parisina. En otoño de 1674 Leibniz escribe De Constructione, donde se resumen algunos de las motivaciones de Leibniz para crear su AS. En este artículo Leibniz lidia principalmente con la relación entre el álgebra y la geometría sintética, además de tratar la constructibilidad con regla y compás y con el problema, también tratado por Newton, de la supuesta mayor naturalidad que poseen las líneas rectas y circunferencias con respecto a otras figuras (De Risi, 2007, 53). También en París escribe otros textos como el Dissertatio exoterica de statu praesenti et incrementus novissimis deque usu in geometria o el De magnitude y Generatio quidem rectae et circuli, redactados justo antes de abandonar la capital francesa en 1676.
Sin embargo, tras su estancia en París, Leibniz sigue desarrollando el AS. Tomemos, por ejemplo, su Characteristica geometrica (1677), uno de los primeros tratados en los que Leibniz presenta su método geométrico de un modo más maduro y cercano a la carta 12. Para comenzar a explicar este método, primero Leibniz debe mostrar cómo funciona la expresión y representación simbólica de las figuras geométricas más comunes. Por ello, expone el modo de representar una línea recta, expresando sus puntos individuales mediante las letras en mayúsculas A, B, etc., y las magnitudes con letras minúsculas. De este modo, una línea (figura 1) se expresa señalando la relación que poseen la serie de puntos que la componen, los cuales se representan como , de modo que para expresar la línea recta B utiliza.
![]()
Figura 1. OFC 7B, 426.
Igualmente, para representar el círculo (figura 2), dado el punto A invariable, tenemos . De este modo, el arco del círculo sería expresado por .
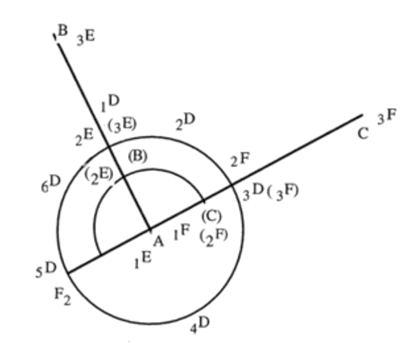
Figura 2. OFC 7B, 427.
Por otro lado, para representar un ángulo (figura 3), supongamos las rectas y , así como el arco. De ese modo, tenemos que ‡ , siendo el ángulo igual a .
Leibniz también define en este texto cómo saber que el punto se encuentra en cualquier punto de la recta; la definición del ángulo recto; y la igualdad de un ángulo recto con cualquier otro (OFC 7B, 426-428). Pero también da un salto cualitativo al explicar el movimiento al señalar que, según la figura 3, el movimiento del punto D produce la recta , donde . De este modo, podemos comprobar el recorrido realizado por el movimiento de la recta con la secuencia . De este modo, la recta es igual a , del mismo modo que es igual a .
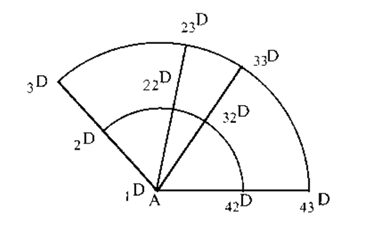
Figura 3. OFC 7B, 426.
Leibniz acude también a la noción de semejanza, la cual define como dos figuras indiscernibles en caso de que las encontremos por separado y con la misma proporción. Por ello “son semejantes las [figuras] que tienen las partes correspondientes proporcionales” (OFC 7B: 429). Partiendo de esta noción, Leibniz demuestra que o expresión analítica de una superficie o de un sector es igual a o expresión analítica del mismo sector. Se puede comprobar la similitud de ambas expresiones en que solamente se diferencian en los caracteres elegidos, pero no en la relación entre ellos, por lo que “su discriminación no puede ser más que sensible y no racional” (OFC 7B, 429).
A partir de aquí Leibniz pone en marcha una de las metas del AS: superar la geometría euclídea, es decir, demostrar los axiomas de Euclides. En este caso, demuestra el axioma de que todos los ángulos rectos son iguales.
[U]n ángulo recto es aquel que, con una recta forma respecto a otra recta un ángulo igual a cada lado, luego la recta respecto a la cual se produce el ángulo a ambos lados es el diámetro, pues el diámetro corta un círculo en dos partes iguales con una recta que pasa por el centro y que se comporta del mismo modo a ambos lados. Luego dos rectos contienen conjuntamente un semicírculo y un recto, un cuadrante de círculo, luego todos los ángulos rectos son iguales. Así hemos demostrado el Axioma de Euclides (OFC 7B, 430).
Leibniz desea proceder del mismo modo con el resto de axiomas euclídeos, así como con los añadidos en posteriores ediciones por Clavius y otros editores, siempre sin necesidad de figuras. Tras ello Leibniz presenta definiciones del arco del círculo, el ángulo rectilíneo, el ángulo recto, los ángulos consecutivos entre sí, la recta, dos rectas que concurren, y la línea recta.
En la edición de La caractéristique géométrique (Leibniz, 1995) encontramos también un texto sin fecha relacionado con el AS, pero que muy probablemente pertenece a esta época anterior al envío a Huygens, al que Echeverría ha titulado Generación de la recta y del círculo. En él, Leibniz muestra la estrecha conexión del AS con el problema del continuo y con el desarrollo paralelo del cálculo infinitesimal sin necesidad de acudir a la experiencia ni tampoco a la imaginación, sino solamente a la razón, que es la única capaz de presentar demostraciones en su sentido más estricto. Esta relación la expresa Leibniz al explicar que para demostrar el movimiento de un cuerpo es necesario demostrar primeramente que el cuerpo “puede comportar una infinidad de puntos inmóviles situados sobre un mismo continuo” (Leibniz, 1995, 69).
Durante la segunda mitad de 1679 comprobamos que Leibniz aumenta la producción de artículos dedicados al AS: muestra de ello es el artículo que De Mora ha titulado Definiciones y que Echeverría llama Ensayos para reducir algunos axiomas y proposiciones de Euclides a caracteres, escrito entre febrero y agosto de 1679; y también los cinco manuscritos llamados Characteristica geometrica con fecha del 1/11 de agosto de 1679, que contienen mejoras conceptuales de las nociones presentadas anteriormente, como la definición de punto, línea, recta, plano, superficie, etc. Especial atención tenemos que prestarle al último de estos manuscritos que De Mora ha titulado Los caracteres son cosas con las que se expresan las relaciones de otras cosas entre sí, que contiene una exposición larga y detallada del AS con hasta 108 proposiciones distintas. ¿Qué encontramos de nuevo en él que no hayamos visto en los textos anteriores? Principalmente, la justificación del uso de los caracteres como símbolos fundamentales en esta nueva geometría:
Cuanto más exactos son los caracteres, es decir, cuantas más relaciones entre las cosas muestran, mayor utilidad proporcionan, y cuando muestren todas las relaciones de las cosas entre sí, del modo que lo hacen los caracteres de la aritmética que yo he utilizado, no habrá nada en la cosa que no pueda ser aprehendido (OFC 7B, 440).
Por ello, debemos recordar que la finalidad del AS no es solamente la mera representación situacional fuera de la visión absolutista de la geometría, sino que también es una forma de aprehender los cuerpos:
En cuanto podamos representar exactamente mediante letras las figuras y los cuerpos, no sólo avanzaremos maravillosamente en Geometría, sino también en Óptica, en Phoronómica, en Mecánica [y todas las artes relacionadas...]3, en todo el universo que está sujeto a la imaginación; lo trataremos con un método seguro y semejante al análisis, y produciremos con este arte maravillosa, invenciones de maquinas que no serán en el futuro más difíciles que las construcciones de los problemas de la geometría (OFC 7B, 442).
Tal y como podemos comprobar, Leibniz desarrolla y mejora el AS durante varios años. Existe, por tanto, una justificación teórica suficiente como para no etiquetar a esta nueva geometría como promesas sin fundamento por parte de Leibniz, tal y como afirmó Huygens. Sin embargo, estos fundamentos teóricos, tal y como veremos, no se encuentran debidamente contextualizados en la comunicación del AS en carta a Huygens.
3. La presentación del analysis situs a Huygens
Pasemos a analizar de qué modo Huygens recibe el AS en la carta 12 de su correspondencia con Leibniz. Para ello debemos señalar el contexto anterior a dicha carta: la número 11 fue escrita por Huygens en junio de 1676, por lo que Leibniz y Huygens llevan más de tres años sin contacto después de que Leibniz abandonase París.
Primeramente, debemos insistir en que la carta 12, escrita el 8/18 de septiembre de 1679 (AA III, 2, n.347: 840-850), es la primera noticia que recibe Huygens del AS. Sabemos que Huygens no conoce su existencia porque Leibniz le explica en la carta 12 de qué trata este método sin suponer en Huygens ningún conocimiento previo, como sí supone al referirse en esta misma carta, por ejemplo, a la cuadratura aritmética, tema tratado anteriormente en la carta 3 (AA III, 1, n.39). Esta primera noticia sobre la existencia de su nuevo método geométrico está dividida en dos partes: por un lado, tenemos el comentario del AS que Leibniz realiza en la carta 12 dirigida a Huygens; y, por otro, el artículo que Leibniz adjunta a esta carta, donde presenta un resumen del AS desarrollado en los últimos años.
La primera referencia al AS por parte de Leibniz dentro de la carta 12, debido a su brevedad, podemos reproducirla en su totalidad:
Mas después de todos los progresos que he hecho en estas materias [se refiere Leibniz a la cuadratura aritmética, a sus avances con las raíces irracionales en las ecuaciones, etc.], no estoy contento con el álgebra, pues no da ni los medios más cortos, ni las más bellas construcciones de Geometría. Esto es porque, cuando se trata de esto, creo que nos hace falta aún un análisis propiamente geométrico o linear que exprese directamente el espacio al igual que el álgebra expresa magnitudes. Y creo haber visto el medio, y que se podría representar las figuras e igualmente las máquinas y sus movimientos con caracteres, tal y como el álgebra representa los números o tamaños; y voy a enviarle un ensayo que me parece considerable; no hay nadie que pudiese juzgarlo mejor que usted, Señor, y vuestra opinión me dirigirá mejor que la de muchos otros (AA III, 2, n.346, 846).
Este breve comentario en la carta 12 está precedido por una explicación sobre el método inverso de tangentes, la cuadratura aritmética, la resolución de raíces irracionales y la aritmética de Diofanto; y le sucede una larga explicación sobre la utilidad del fósforo (pues Leibniz adjunta un trozo de este elemento también a esta carta) con referencias a la posibilidad del fuego perpetuo, para terminar con una postdata en la que solicita indirectamente a Huygens su ayuda para poder conseguir un puesto de empleo en la Académie des sciences parisina. Ello nos muestra que el comentario de Leibniz sobre el AS se encuentra presentado entre un confuso conjunto de distintos temas que impiden que Huygens vea con claridad qué quiere conseguir Leibniz concretamente con esta nueva característica geométrica. Es posible que, si Leibniz hubiese contextualizado con mayor rigor el AS, habría conseguido una mínima comprensión por parte de Huygens. Pero Leibniz parece considerar que este breve comentario es suficiente, junto con el adjunto, donde detalla el apartado técnico de esta nueva geometría.
El artículo adjunto a la carta 12 (AA III, 2, n.347, 851-860), centrado completamente en el AS, comienza afirmando que la nueva característica podrá presentar directamente ante el espíritu de forma exacta y “al natural” todo aquello que depende de la imaginación; así como que el álgebra se refiere a las magnitudes pero que no expresa el situs, es decir, la situación de las figuras, ni tampoco los ángulos ni el movimiento de los cuerpos. De ello se deduce que el álgebra es una herramienta imperfecta para representar adecuadamente figuras que poseen un situs y que fenoménicamente son modificadas en su movimiento. Y hasta tal punto es imperfecto el álgebra que necesita dar por supuestos los axiomas euclídeos, mientras que el AS que él presenta “empuja el análisis hasta el final” (AA III 2, n.347, 852).
Además de prometer que mediante el uso de letras del alfabeto podrán describirse cualquier tipo de máquinas que podamos imaginar, Leibniz afirma que con este método se podrán describir incluso plantas y la estructura de los animales, dando a entender que el AS, desarrollado en todo su potencial, podría servir como una herramienta que geométricamente podría describir a los seres vivos cuyos cuerpos están gobernados por principios biológicos aparte de mecánicos. Del mismo modo, si bien no es algo que Leibniz señale explícitamente, el AS posee una cimentación metafísica como una “verdadera ciencia del espacio, entendido éste como la combinatoria infinita de las relaciones de situación posibles” (Ruiz-Gómez, 2019, 22). Por tanto, vemos que aunque habitualmente se resalte la posibilidad de describir figuras mediante símbolos, esta no es su única finalidad:
[...] esta es la menor de las utilidades de esta característica, pues si no se trata más que de la descripción, siempre será preferible, cuando se pueda y se quiera hacer el esfuerzo, tener las figuras e incluso los modelos, o más bien los originales de las cosas. Mas su utilidad principal consiste en las conclusiones y razonamientos que se pueden hacer mediante las operaciones de los caracteres, que no se podrían expresar mediante figuras (y aún menos mediante modelos) sin multiplicarlas demasiado o sin emborronarlas con un gran número de puntos y de líneas, de tal modo que se estaría obligado a hacer un gran número de tentativas inútiles; mientras que este método nos conduciría de forma segura y sin esfuerzo, al no hacerse las tentativas más que en caracteres. Creo que se podría manejar por este medio la mecánica, casi como la geometría (OFC 7B, 488-489).
La ambición del AS supone, por lo tanto, incluso poder manejar los problemas mecánicos mediante el método de la utilización de símbolos sin necesidad de atender a las figuras dibujadas. Hasta tal punto muestra Leibniz la ambición de la característica geométrica que afirma que no cree que se pueda llegar muy lejos en física sin encontrar “un atajo similar para aliviar la imaginación”, a lo que añade que este ensayo “bastará por lo menos para hacer mi propuesta más creíble y fácil de concebir” (OFC 7B, 489).
El apartado técnico del adjunto a la carta 12 comienza exponiendo que para hacer referencia a los lugares utiliza las letras del alfabeto A, B, etc., los cuales expresan puntos dados, mientras que utiliza X, Y, etc., para expresar los puntos buscados. Y para realizar cálculos Leibniz utiliza la congruencia, representada por el símbolo , concepto primordial en el AS. La congruencia se presenta cuando dos figuras son isométricas, es decir, cuando son equivalentes en cuando a figura, orientación o posición, sin importar que las figuras tengan una rotación distinta. En ese sentido, cuando dos figuras son isométricas, son representadas por los mismos caracteres. Para mostrar esto, Leibniz propone a Huygens el ejemplo de dos triángulos (figura 4) que tienen las mismas características pero que poseen una orientación distinta:
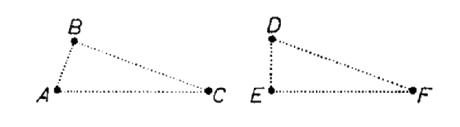
Figura 4. AA III 2, n.347, 854.
La situación entre los puntos A, B y C del triángulo al que llamamos ABC es la misma que poseen los puntos D, E y F en el triángulo DEF. Por ello, se dice que los puntos de ambos triángulos son congruentes, lo cual se representa mediante ABCDEF. Ello queda más claro si eliminamos el dibujo de las figuras y nos quedamos tan sólo con los puntos definidos, de modo que se muestra que para la expresar la congruencia de estos puntos dados no es necesaria la existencia de la figura, sino que se puede expresar simplemente con la operación realizada mediante caracteres.
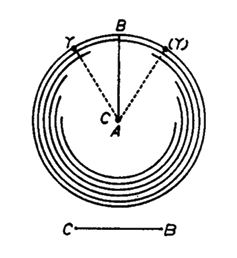
Figura 5. AA III 2, n.347, 855
Leibniz prosigue exponiendo la superficie de la esfera (figura 5), que estará representada como el lugar de todos los Y, en una esfera cuyo centro es A y el radio AY. Siguiendo la representación por caracteres, el lugar de todos los Y se expresa ABCY.
Igualmente, Leibniz define el plano (figura 6), “es decir, el lugar de todos los puntos del mundo, cada uno de los cuales es” (OFC 7B, 491) como AXBX, dados los puntos A y B y teniendo a X como incógnita. En esta figura, X debe tener la misma situación con respecto tanto con A como con B, es decir, AX debe ser congruente con BX. De este modo, todos los puntos del plano satisfacen la cuestión, pues todo punto posible X sigue ofreciendo AXBX.
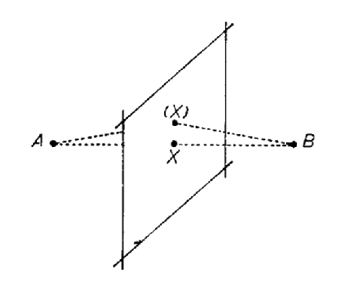
Figura 6. AA III 2, n.347, 856.
Del mismo modo, define la circunferencia señalando que en la figura 7, siendo ABCABY, la circunferencia estará formada por el lugar de todas las Y posibles, es decir, que teniendo los puntos ABC, se demanda un punto Y que posea la misma situación que posee C. Como puede observarse, el número de puntos Y posibles en la circunferencia son infinitos, y la circunferencia estará formada por la totalidad de los infinitos puntos Y. Tal y como podemos comprobar, esta forma de representar la circunferencia no necesita presuponer el plano, como sí necesitaba Euclides.
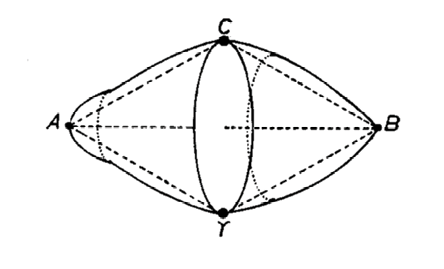
Figura 7. AA III 2, n.347, 857.
Por último, Leibniz define la recta. En este caso, dando tres puntos A, B, C (figura 8), buscamos un punto Y, el cual debe tener la misma situación respecto a A, al igual que con respecto a B y a C. Todos los puntos Y que satisfagan esta cuestión formarán una recta infinita.
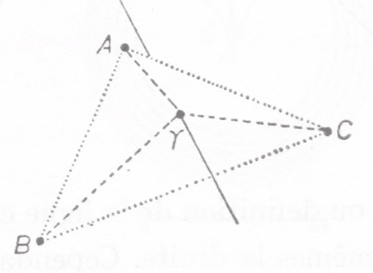
Figura 8. AA III 2, n.347, 858.
Leibniz afirma que todas estas definiciones se pueden presentar de otras maneras. De hecho, en los borradores anteriores las definiciones de estas figuras básicas de la geometría, como hemos visto, poseen matices distintos, pero afirma Leibniz que estas formas son las «más simples y fecundas» (OFC 7B, 494). Y termina Leibniz con las siguientes palabras:
Sólo me queda añadir una observación, que veo que es posible extender la característica hasta las cosas que no están sujetas a la imaginación: pero esto es demasiado importante y va demasiado lejos para que pueda explicarme sobre ello en pocas palabras (OFC 7B, 495).
El contexto del envío del AS a Huygens, especialmente en su presentación en la carta 12 y en las alusiones a representar mediante caracteres a seres vivos en el adjunto, facilita, tal y como hemos podido ver, la incomprensión de Huygens. Pero además, dentro del adjunto a la carta 12, es muy posible que estas últimas palabras enviadas a Huygens engrandeciesen más si cabe la confusión, al hacer referencia a “hasta las cosas que no están sujetas a la imaginación”, así como el explicar que lo enviado “es demasiado importante” y “va demasiado lejos” como para explicarse en pocas palabras. Si bien no hay duda de la honestidad intelectual de Leibniz, pues sus promesas están justificadas a la luz del desarrollo del AS anterior a la carta enviada a Huygens, la exposición y el resto de los contenidos de la carta 12 y su adjunto no facilita la comprensión del método por parte de Huygens, por lo que es muy probable que ello ocasionase que Huygens no dedicase tiempo suficiente al apartado técnico, el cual resulta confuso (sobre todo sin tener Huygens acceso al desarrollo previo del AS), y además, no llega a mostrar de qué modo se llevarían a cabo las promesas señaladas por Leibniz.
4. Bellos deseos
En la carta 13, enviada el 10/20 de octubre de 1679 (AA III, 1, n.359, 873-877; tan solo un mes después de la carta 12), ante la falta de respuesta de Huygens, Leibniz envía a Huygens un breve resumen del contenido de la carta anterior, donde señala que el AS es un método que sigue “figuras vacías, lo cual alivia la imaginación”. La respuesta de Huygens se demora hasta el 22 de noviembre de 1679, en la carta 14 (AA III, 1, n.351, 886-890). En ella, refleja de un modo directo su incomprensión:
He examinado atentamente lo que me ha mandado respecto a vuestra nueva característica, mas para serle franco no comprendo, por lo que me dice, que pueda fundar tantas esperanzas. [...] En resumen, no veo cómo podrá usted aplicar vuestra característica a todas estas cosas diferentes que parece que usted quiere reducir, como las cuadraturas, la invención de las curvas por la propiedad de las tangentes, las raíces irracionales de las Ecuaciones, los problemas de Diofanto, las más cortas y bellas construcciones de problemas geométricos. Y, lo que me parece más extraño, la invención y explicación de las máquinas. Le digo ingenuamente, esto no son en mi opinión más que bellos deseos, y me harían falta otras pruebas para creer que hubiese realidad en lo que usted avanza. Por tanto, no me guardo de decir que usted se ha engañado, conociendo la sutilidad y profundidad de vuestro espíritu. Voy a suplicarle solamente que la grandeza de las cosas que usted busca no le haga diferir de darnos aquellas que usted ya ha encontrado, como esta cuadratura aritmética y eso que usted ha descubierto para las raíces de las ecuaciones que van más allá del cubo, si usted mismo está satisfecho (AA III, 2, n.359, 889).
Esta respuesta es mucho más negativa de lo que Leibniz parecía esperar, no solamente porque el adjunto a la carta 12 estaba destinado a demostrar las capacidades científicas del joven Leibniz, sino porque la opinión de su antiguo maestro (y todavía director de la Académie des sciences) daña el orgullo científico de Leibniz, denominando “bellos deseos” a la ambición presente en el AS.
Leibniz responde en la carta 15 (AA III, 1, n.361, 892-904), escrita a finales de noviembre/principios de noviembre, es decir, presumiblemente nada más recibir la carta 14 de Huygens, lo cual muestra la urgencia de Leibniz en responder su crítica. En esta carta, Leibniz defiende el AS afirmando que “las raíces irracionales y el método de Diofanto, no tienen nada en común con esta característica de la situación” (AA III 2, n.361, 897) y que su cálculo ofrece lo que no ofrece el álgebra, poniendo como ejemplo que siendo la ecuación de la circunferencia , es necesario dibujar la circunferencia para explicar qué son x e y, mientras que con el AS esta representación es una tarea que se realiza directamente y sin la necesidad de la figura, añadiendo que esto es un ejemplo y que igualmente mediante el AS lo mismo puede realizarse con cualquier figura mediante las definiciones que incluye el artículo adjunto a la carta 12.
La siguiente carta, la número 16 en su correspondencia (AA III, 1, n.364, 907-909), no tiene contenido relativo al AS, pues es un envío por parte de Leibniz de instrucciones para encender el fósforo, junto con otros comentarios marginales. No es hasta el 11 de enero de 1680, en la carta 17 (AA III, 3, n.4, 48-49), cuando Huygens vuelve a responder de la siguiente manera:
Respecto a los efectos de vuestra característica, veo que usted persiste en ser persuadido, mas como usted mismo dice, los ejemplos afectarían más que los razonamientos. Esto es porque le pido los más simples, pero apropiados para convencer mi incredulidad, pues el de los lugares, lo reconozco, no me parece de este tipo (AA III, 3, n.4, 48-49).
Es decir, el ejemplo enviado por Leibniz en el adjunto de la carta 12 y su insistencia en cartas posteriores no le parece a Huygens suficiente para poder comprender la utilidad de la característica geométrica de Leibniz, pidiéndole los ejemplos más simples posibles, algo que Leibniz ya pensaba haber hecho, pues el adjunto a la carta 12 pretende ser una síntesis del AS.
A partir de aquí vemos un cambio de estrategia por parte de Leibniz: en lugar de insistir en la utilidad del AS, tras la opinión negativa de Huygens, Leibniz envía junto con la carta 18 (AA III, 3, n.22, 71-73) otro artículo adjunto (AA III, 3, n.23, 73-78), si bien en este caso su contenido no está centrado en el AS sino en su método inverso de tangentes. Esto parece apoyar una hipótesis que debe ser probada en otra investigación, que es la probabilidad de que Leibniz estuviese presentando esta variedad de métodos y avances científicos tanto en la carta 12 como en la carta 18 con la finalidad de conseguir un puesto remunerado en la Académie des sciences. Debemos señalar, sin embargo, que a pesar de que el tema principal de la carta 18 es el método inverso de tangentes, Leibniz dedica unas brevísimas palabras a la opinión de Huygens sobre el AS:
Para dar un ensayo de mi característica he elegido los lugares [situs] porque todo el resto se determina por sus intersecciones; y porque la generación de todos los otros lugares depende de los más simples que he dado. De este modo creo haber echado los verdaderos cimientos (AA III, 3, n.22, 71).
Se puede comprobar, por otro lado, que el borrador de la carta 18, centrado en el método inverso de tangentes, es mucho más amplio que la carta que finalmente Leibniz decide enviar a Huygens. ¿Puede ser el motivo de ello el deseo de Huygens de que Leibniz le haga llegar los ejemplos más sencillos? Creo que todos los indicios nos llevan a pensar que habría que responder afirmativamente.
A la postre, las palabras de Leibniz sobre el AS en la carta 18 fueron las últimas enfocadas en esta nueva geometría durante la correspondencia con Huygens, a pesar de que la carta está escrita a principios de 1680, y de que la correspondencia se alarga hasta 1695.
En definitiva, tras haber analizado los primeros desarrollos del AS, el contexto que rodea a la carta 12 y su adjunto, así como la correspondencia con Huygens desde la carta 12 a la 18, creemos que los datos indican que la incomprensión de Huygens puede estar motivada por las siguientes causas: (a) las promesas de Leibniz, infundadas a ojos de Huygens; (b) el hecho de que, si bien Leibniz era tenido en gran consideración por Huygens, todavía tenía que demostrar a la comunidad científica sus capacidades en el ámbito de las matemáticas, mínimas antes de su llegada a París; (c) la mezcla de asuntos presentados en la carta 12 alrededor del AS: el fósforo, el fuego perpetuo, el cálculo infinitesimal, la aritmética de Diofanto o el método de inverso de tangentes, entre otros. Del mismo modo, el apelar a la palabra “cálculo” en varias ocasiones en las cartas 12, su adjunto, y la carta 13, podría aumentar la confusión de Huygens entre el AS y el cálculo infinitesimal; y (d) la urgencia mediante la cual Leibniz presenta su método, con la muy probable finalidad de conseguir un puesto remunerado en la Académie des Sciences. Esto podía ocasionar que Huygens no viese con suficiente seriedad la nueva geometría de Leibniz.
5. Tras la opinión negativa de Huygens
A pesar del cambio que Leibniz realiza en el hecho de enviar a Huygens, en la carta 18, un adjunto sobre el método inverso de tangentes en lugar de un adjunto mejorando la comunicación precedente a Huygens del AS, existen al menos dos textos escritos en enero de 1680 (fecha también de la carta 18) en los que Leibniz sigue desarrollando el AS. En el primero de ellos, titulado De primis geometriae elementis, Leibniz presenta definiciones de las nociones de extensión, espacio, recta, o plano, sin utilizar una sola figura. Creemos que es bastante llamativo que Leibniz realice este ejercicio de definiciones sin utilizar ninguna figura justo en el momento en el que recibe la carta 17 de Huygens, que contiene la segunda respuesta negativa sobre el AS y que está escrita el 11 de enero de 1680 según el calendario gregoriano, que corresponde con el comienzo del año 1680 en el calendario juliano bajo el que Leibniz escribe. Si Leibniz responde el 26 de enero siguiendo el calendario juliano, vemos que ha tenido aproximadamente 25 días para recibir la carta de Huygens, escribir su respuesta y desarrollar estos dos artículos de enero de 1680. No olvidemos la usual demora con la que se recibían las comunicaciones epistolares en la época, por lo que el tiempo dedicado por Leibniz a esta tarea (la escritura de la carta 18 a Huygens, de su adjunto, y de los dos manuscritos fechados en enero de 1680), es mínimo, lo cual indica la urgencia de Leibniz.
¿Es De primis geometriae elementis un texto escrito como respuesta a la segunda opinión negativa de Huygens? Las fechas coinciden y la simpleza de este último texto a la hora de presentar las definiciones puede deberse al deseo de Leibniz de satisfacer a Huygens. Leibniz afirma en esta obra que hay dos cosas por estudiar en la geometría: la extensión y la situación (situs). La extensión es definida como un continuo en el que se pueden delimitar las partes que existen simultáneamente, pero que a su vez las partes son solamente delimitadas mentalmente y no de un modo fáctico (pues entonces habría saltos en la naturaleza, lo cual no es admisible para Leibniz). Por otro lado, la situación es definida como la posición de una cosa que permite imaginar que existe de una manera determinada al mismo tiempo que es extensa (Leibniz, 1995, 277). Cabe destacar la definición de espacio de Leibniz en este texto, del que dice que es aquello sobre lo que solamente se puede decir, si lo consideramos en sí mismo, que es un extenso (extensum); y que es indeterminado, porque de ser de otro modo, para definir el espacio deberíamos tener en cuenta aquello que delimita al espacio: “El espacio es [...] lo más simple que hay en cuanto a extensión, el punto lo que hay más simple en cuanto a situación” (Leibniz, 1995, 279). Estos estudios que Leibniz desarrolla sobre su concepción de espacio muestran una conexión con su metafísica madura, su perspectivismo y su ontología:
The situation of a body with respect to all other bodies simultaneous with it is thus given by all the angles and distances from the body (now thought of as a point) to all the other bodies co-existent with it. This is a representation of all those co-existents at such a point; God creates each substance as an actualization of such successive representations, as we saw above. The substances are metaphysical points, and the mathematical points from which the situations of all the other bodies are represented in the substances are their points of view. These considerations help explain the connection between Leibniz’s Analysis Situs and his theory of space, and how both are related to his shift to an ontology of individual substances whose perceptions are representations from a given point of view (Arthur, 2013, 517).
Por último, el segundo manuscrito, también fechado en 1680 y titulado De calculo algebraico et constructiones lineares optime conciliandis, es un texto más complejo que el anterior, en el que Leibniz se dedica a estudiar cómo traducir el cálculo algebraico en el lenguaje del AS. Sin embargo, la complejidad de este texto nos hace dudar de que estuviese siendo preparado para Huygens. Lo que sí sabemos con seguridad es que tras la carta 18 no vuelve a aparecer en la correspondencia con Huygens ninguna discusión sobre el AS, y Leibniz no retoma estas cuestiones hasta 1692.
6. Conclusiones
Tras analizar el desarrollo original del AS, la carta 12, su adjunto, y las cartas posteriores intercambiadas entre Leibniz y Huygens, creemos que hay evidencia suficiente como para defender la hipótesis de que Leibniz no presentó adecuadamente este nuevo método a Huygens y que ello ha sido un factor determinante para la incomprensión de Huygens. El hecho de que la carta 12 presentase el AS no como tema principal, sino como uno más dentro de un conjunto de temas adicionales, como la cuadratura aritmética, las raíces irracionales, la aritmética de Diofanto, el cálculo infinitesimal, el fuego perpetuo y el uso del fósforo, no facilitó que Huygens comprendiese que el AS era un método original, prometedor, y sobre todo distinto al resto de temas tratados en la carta. Por su parte, el adjunto a la carta 12 posee un apartado técnico que, si bien introduce esta nueva geometría, resulta ser una introducción confusa y poco desarrollada. Del mismo modo, las promesas de Leibniz en dicho adjunto, las cuales señalan que incluso se podría representar la estructura de animales y plantas mediante caracteres, pero sin señalar ningún ejemplo de cómo podría realizarse esta tarea, tampoco facilitaron que la opinión de Huygens mejorase.
Ante ello, cabría preguntarse algunas cuestiones de difícil respuesta: ¿habría Huygens comprendido el AS de haberlo presentado Leibniz de un modo más apropiado, quizá dándole la importancia que merecía en la carta, en lugar de estar incluido entre diferentes temas que tenían poco que ver con esta nueva geometría? ¿Habría estado Huygens más inclinado a aceptar la utilidad del AS, o habría dedicado mayor esfuerzo a comprender el adjunto a la carta 12 de haber convencido Leibniz a otros coetáneos suyos? ¿O habría ocurrido como con el cálculo infinitesimal, que fue primeramente rechazado para al final acabar Huygens rindiéndose ante la evidencia de su utilidad?
Referencias
Antognazza, M.R. (2009). Leibniz: An Intellectual Biography, Cambridge: CUP.
Arthur, R. (2013). Leibniz’s Theory of Space. Foundations of Science, 18(3), pp. 499-528.
Couturat, L. (1969), La logique de Leibniz: D’après des documents inédits, Hildesheim: Georg Olms.
De Mora, M. (2018). «Leibniz crítico de Euclides. El método del analysis situs», Quaderns d’historia de l’enginyeria, 16, pp. 93-107.
De Risi, V. (2018). «Analysis Situs, the Foundations of Mathematics, and a Geometry of Space», en: Antognazza, M.R. (ed.): The Oxford Handbook of Leibniz, Oxford: OUP, pp. 247-258.
De Risi, V. (2011). «Leibniz’s analysis situs and the Localization of Monads», en: Breger, H., Herbst, J.,y Erdner, S. (eds.), Natur Und Subjekt: Akten des IX Internationalen Leibniz-Kongresses, Hanover: Hartmann, pp. 208-16.
De Risi, V. (2007), Geometry and Monadology. Leibniz’s Analysys situs and Philosophy of Space, Dordrecht: Springer.
De Risi, V. (2005). Leibniz on Geometry: Two Unpublished Texts with Translation and Commentary. The Leibniz Review, 15, pp. 127-132.
Echeverría, J., y De Mora, M. (2016). Leibniz crítico de Euclides. El método del Analysis Situs. Kairos, Journal of Philosophy & Science, 16(1), pp. 99-123.
Echeverría, J. (1995), «Introducción», en: Leibniz, G. W.: La caractéristique géométrique, París: Vrin, pp. 7-44.
Echeverría, J. (1984), «La Geometría Leibniciana: de la Prespectiva al Analysis Situs», en: Sociedad Española de Historia de las Ciencias y de las Técnicas (ed.): Actas II Congreso de la Sociedad Española de Historia de las Ciencias, Madrid: SEHCYT, pp. 69-78.
Echeverría, J. (1979), «L’Analyse Géométrique de Grassmann et ses rapports avec la Caractéristique Géométrique de Leibniz», Studia Leibnitiana, 11(2), pp. 223-273.
Freudenthal, H. (1972), «Leibniz und die Analysis Situs», Studia Leibnitiana, 4(1), pp. 61-69.
Huber, K. (1951), Leibniz, Berlín: De Gruyter.
König, S. (1752), Appel au public du jugement de l’Académie Royale de Berlin sur un fragment de la lettre de M. de Leibnitz cité par M. Koenig, Leiden: Elie Luzac.
Leibniz, G.W. [OFC] (2007ss), Obras filosóficas y científicas. Nicolás, J.A. (ed,), Granada: Comares.
Leibniz, G.W. (1995), La caractéristique géométrique, Echeverría, J. (ed.), París: Vrin,
Leibniz, G.W. (1968), Scritti di Logica, Bologna: Zanichelli.
Leibniz, G.W. [AA] (1923ss), Sämtliche Schriften und Briefe, Berlín, Darmstadt, Deutschen Akademie der Wissenschaften zu Berlin.
Martin, D.J. (1983). Leibniz’s conception of analysis situs and its relevance to the problem of the relationship between mathematics and philosophy, PhD Thesis, Atlanta, GA, Emory University.
McDonough, J.K. (Draft, 2021). «Space, Monads, and Incompossibility», en: Rutherford, D. (ed.), Oxford Studies in Early Modern Philosophy, vol. 10, Oxford, Oxford University Press.
Ruiz-Gómez, L. (2019), «Leibniz y el analysis situs. Los infinitesimales como estructuras situacionales», Anuario filosófico, 52(3), pp. 1-23.
1 Respecto a la discusión sobre el problema de la espacialidad en las relaciones entre mónadas, ver: McDonough, Draft, 2021. Arthur también ha señalado el problema de la unión entre la teoría del espacio leibniziana con el perspectivismo en la mónada y el cuerpo orgánico que le corresponde (2013, 518).
2 “The profound geometrical research Leibniz begins to undertake going into the foundational core of ancient geometry will provide him with an incredible arsenal of metaphysical arguments with which he can start to build his own philosophy of space and graft it on his mature monadological theory. His subsequent writings on the analysis situs [...] will lead step by step towards the Initia rerum mathematicarum metaphysica and another cluster of similar papers on situational analysis which intertwine with the writing of the Monadologie and the letters to Clarke” (De Risi, 2005, 128).
3 Frase tachada por Leibniz en el manuscrito.