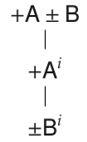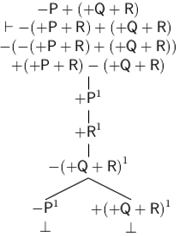Una traducción terminista de la lógica natural de Moss

A Terministic Translation of Moss’ Natural Logic

J.-MARTÍN CASTRO-MANZANO*

---

Resumen: En esta contribución presentamos una traducción de la lógica natural de Moss a la lógica de términos de Sommers usando un método de árboles. El resultado de esta traducción muestra que la lógica de términos de Sommers se encuentra más allá de la frontera de los sistemas tipo Peano-Frege, Church-Turing y Aristóteles pero mantiene el poder expresivo de los sistemas que habitan dentro de tales límites. Esto sugiere que la lógica de términos puede ser útil para un proyecto de lógica natural.

Palabras clave: Razonamiento en lenguaje natural, lógica de términos, árboles semánticos.

Abstract: In this contribution we present a translation from Moss’ natural logic to Sommers’ term logic by using a tableaux method. The result shows Sommers’ term logic lies beyond the Peano-Frege, Church-Turing, and Aristotle frontiers while maintaining the inferential and expressive powers of the systems that inhabit such limits. This suggests that term logic might be instrumental for a natural logic project.

Keywords: Natural language reasoning, term logic, semantic trees.

1. Introducción

En este trabajo intentamos alcanzar una meta sencilla: ofrecer una traducción de la lógica natural de Moss a la lógica de términos de Sommers usando un método de árboles. El resultado de esta traducción muestra que la lógica de términos de Sommers es un sistema alternativo a la lógica natural de Moss que i) se encuentra más allá de la frontera de los sistemas tipo Peano-Frege, Church-Turing y Aristóteles pero que ii) mantiene el poder expresivo de los sistemas que habitan dentro de los límites de tales fronteras —más adelante daremos detalles de lo que significa habitar estos confines.

Este resultado, como veremos, sugiere que las lógicas de términos, lejos de estar condenadas a ser un episodio superado de la historia de la lógica, pueden ser usadas adecuadamente en la implementación de un proyecto de lógica natural. Para alcanzar nuestra meta y exponer el resultado obtenido procedemos de la siguiente manera: primero hacemos una introducción general a la lógica natural de Moss y a la lógica de términos de Sommers (§2), posteriormente presentamos nuestra traducción (§3) y, por último, hacemos algunas observaciones sobre los resultados obtenidos (§4).

2. La lógica natural de Moss y la lógica de términos de Sommers

2.1. Aspectos generales de la lógica natural de Moss

De acuerdo con Moss (2015), la raison d’être de la lógica es el estudio de la inferencia en un lenguaje natural. Ahora bien, para estudiar la inferencia en un lenguaje natural es costumbre hacer uso de lenguajes de orden n: la lógica proposicional y la lógica de primer orden (con identidad), por ejemplo, son sistemas lógicos definidos mediante lenguajes de orden 0 y 1 respectivamente.

Aunque el origen de este hábito tiene una historia interesante y compleja (Eklund, 1996), está relacionado, ciertamente, con las ventajas de orden representativo que los lenguajes de primer orden ofrecen frente a sistemas más tradicionales;1 sin embargo, aunque esta elección sintáctica —la de usar sistemas de primer orden— nos es habitual en la docencia, la investigación y la aplicación de la lógica —digamos, es la visión heredada de la lógica (cfr. Castro-Manzano, 2021)—, no hace falta ser hipercríticos para notar que esta visión de la lógica, en efecto, nos puede ser familiar, pero no por ello nos resulta natural. Woods comenta (el énfasis es nuestro):

It is no secret that classical logic and its mainstream variants aren’t much good for human inference as it actually plays out in the conditions of real life —in life on the ground, so to speak. It isn’t surprising. Human reasoning is not what the modern orthodox logics were meant for. The logics of Frege and Whitehead & Russell were purpose-built for the pacification of philosophical perturbation in the foundations of mathematics, notably but not limited to the troubles occasioned by the paradox of sets in their application to transfinite arithmetic. (Woods, 2016: 404).

Ciertamente, si bien la lógica de primer orden (clásica, según Woods) ha sido fundamental para el estudio de la inferencia en general, no deja de extrañarnos que, a pesar de su finalidad original en la fundamentación de las matemáticas, sea utilizada constantemente como una herramienta bona fide para la representación de razonamiento en lenguaje natural. Consideremos, a este efecto, lo que hemos denominado “el reto de Bar-Hillel” (el énfasis es nuestro):

I challenge anybody here to show me a serious piece of argumentation in natural languages that has been successfully evaluated as to its validity with the help of formal logic. I regard this fact as one of the greatest scandals of human existence. Why has this happened? How did it come to be that logic which, at least in the views of some people 2,300 years ago, was supposed to deal with evaluation of argumentation in natural languages, has done a lot of extremely interesting and important things, but not this? (Stall, 1969: 256).

Para Moss, este desajuste entre lógica y lenguaje natural ha tenido dos efectos: una desatención al lenguaje natural y una sobrevaloración de los sistemas de primer orden. Estos efectos son problemáticos lógica y computacionalmente porque, por un lado, los sistemas de primer orden son incapaces de modelar ciertas inferencias interesantes de lenguaje natural, como la simplificación poliádica; y por otro lado, ciertos fragmentos de primer orden son indecidibles.2

Ante esta situación, el proyecto de Moss pretende mostrar que ciertas partes significativas del razonamiento en lenguaje natural pueden llevarse a cabo usando lenguajes de primer orden —con ciertas modificaciones sintácticas, como veremos— pero en sistemas decidibles. Para alcanzar esta meta, Moss propone una serie de sistemas lógicos que se introducen de manera incremental, del sistema más simple al más complejo, y demuestra que cada uno de ellos es completo: a esta serie la llamamos “jerarquía de Moss”. Para los fines de este trabajo, a continuación exponemos la jerarquía de Moss mediante la exposición de su sintaxis y sus reglas de inferencia —por cuestiones de espacio y por las metas de este trabajo, omitimos las pruebas de completud.

La jerarquía de Moss comienza con una lógica que incluye el cuantificador “Todo” (este sistema se llama A por el cuantificador universal, por All). La sintaxis de A depende de un conjunto infinito de sustantivos p, q, r, …, que son útiles para formar enunciados de la forma:

Todo p es q

La semántica de las expresiones de A depende de un modelo M que se define, como es usual, mediante un conjunto M y una interpretación |[p]|⊆M para cada sustantivo p de tal manera que:

M ⊨ Todo p es q si y solo si |[p]|⊆|[q]|.

Y las reglas de inferencia de A son dos:

Tabla 1: Reglas de A

⊢Todo p es p

Todo p es n Todo n es q ⊢Todo p es q

Dada esta información, notar que el sistema A es, en efecto, completo, es trivial. Lo que hace Moss, posteriormente, es agregar nuevas reglas de inferencia al sistema A pero preservando completud. Así, para generar el siguiente sistema, S, Moss introduce el cuantificador “Algún” para producir enunciados de la forma:

Algún p es q

La semántica de este sistema se define, entonces, del siguiente modo:

M ⊨ Todo p es q si y sólo si |[p]|⊆|[q]|.

M ⊨ Algún p es q si y sólo si |[p]|∩|[q]|≠∅.

Y las reglas de inferencia, en consecuencia, son las siguientes:

Tabla 2: Reglas de A y S

⊢Todo p es p		Todo p es n Todo n es q ⊢Todo p es q
Algún p es q ⊢Algún q es p	Algún p es q ⊢Algún p es p	Todo q es n Algún p es q ⊢Algún p es n

Es claro, hasta este punto, cuál es la idea de la jerarquía: todo lo que se puede probar en un sistema inferior (digamos A) se puede probar en un sistema superior (digamos S) pero no a la inversa.

El siguiente sistema, S†, resulta de añadir los átomos complementarios, p, con la interpretación |[p]|=M/|[p]| de tal manera que S† gana expresividad sobre S en la medida en que en S† se pueden expresar los siguientes enunciados que no se pueden expresar en A o en S (de ahora en adelante, todos los sistemas anotados con “†” representan sistemas con negación completa):

Tabla 3: Enunciados de S y S†

S	Todo p es q	S†
	Algún p es q
	Todo p es q = Ningún p es q
	Algún p es q = Algún p no es q
	Algún p es q

En consecuencia, las reglas de inferencia para S y S† son las siguientes:

Tabla 4: Reglas de S y S†

⊢Todo p es p		Todo p es n Todo n es q ⊢Todo p es q	Todo q es q ⊢Todo q es p	Todo q es q ⊢Todo p es q
Algún p es q ⊢Algún q es p	Algún p es q ⊢Algún p es p	Todo q es n Algún p es q ⊢Algún p es n	Todo p es q ⊢Todo q es p	Algún p es p ⊢X

Como se puede apreciar hasta este momento, con estos elementos de la jerarquía, Moss logra reconstruir la semántica y la completud de lo que conocemos como silogística asertórica (vide Apéndice A). Sin embargo, añadiendo variables para representar verbos transitivos —lo cual es una variación sintáctica en un sistema típico de primer orden—, Moss produce un par de sistemas expresivamente más poderosos: los sistemas relacionales R y R†. Para ejemplificar las capacidades expresivas de R y R†, donde r expresa un verbo transitivo, consideremos los siguientes enunciados básicos de R y R†:

Todo p es q := ∀(p, q)

Algún p es q := ∃(p, q)

Todo p hace r a todo q := ∀(p, ∀(q, r))

Todo p hace r a algún q := ∀(p, ∃(q, r))

Algún p hace r a todo q := ∃(p, ∀(q, r))

Algún p hace r a algún q := ∃(p, ∃(q, r))

Ningún p es q := ∀(p, q)

Algún p no es q := ∃(p, q)

Ningún p hace r a todo q := ∀(p, ∀(q, r))

Ningún p hace r a algún q := ∀(p, ∃(q, r))

Algún p no hace r a todo q := ∃(p, ∀(q, r))

Algún p no hace r a algún q := ∃(p, ∃(q, r))

Dada esta sintaxis, las reglas de inferencia de R y R† son las reglas de S y S† más las siguientes reglas, donde p y q varían sobre átomos, c sobre términos y t sobre átomos binarios o sus negaciones:

Tabla 5: Reglas de R y R†

∃(p, q) ∀(q, c) ⊢∃(p, c)	∀(p, q) ∀(p, c) ⊢∀(q, c)
∀(p, q) ∃(p, c) ⊢∃(q, c)	⊢∀(p, p)	∃(p, c) ⊢∃(p, p)
∀(q, c) ∃(p, c) ⊢∃(p, q)	∀(p, p) ⊢∀(p, c)	∃(p, ∃(q, t)) ⊢∃(q, q)
∀(p, ∀(n, t)) ∃(q, n) ⊢∀(p, ∃(q, t))	∃(p, ∃(q, t)) ∀(q, n) ⊢∃(p, ∃(n, t))
∀(p, ∃(q, t)) ∀(q, n) ⊢∀(p, ∃(n, t))	[φ] … ∃(p, p) ⊢φ

Para ilustrar el funcionamiento de estos sistemas consideremos una inferencia (válida) que puede ser modelada en R (pero no en S† o en A):

Tabla 6: Ejemplo de inferencia en R

	Enunciado
1.	Todo perro mira a todo gato.
2.	Todo perro mira a algún ratón.
3.	Algún ratón mira a algún gato.
⊢	Todo perro mira a algún gato.

Los siguientes sistemas en la jerarquía, RC y RC†, resultan de añadir cláusulas relativas a R y R†. Una cláusula relativa es una expresión tal que nos permite ofrecer inferencias (válidas) como las siguientes:

Tabla 7: Ejemplo de inferencia en RC y RC†

	Enunciado
1.	Todos los perros son mamíferos.
⊢	Todos los que temen a los que respetan a los perros temen a todos los que respetan a los mamíferos.

Tabla 8: Ejemplo de inferencia en RC y RC†

	Enunciado
1.	Todos los perros son mamíferos.
⊢	Todos los que temen a los que respetan a algunos perros temen a todos los que respetan a algunos mamíferos.

Tabla 9: Ejemplo de inferencia en RC y RC†

	Enunciado
1.	Algunos perros son mamíferos.
⊢	Algunos que temen a los que respetan a algunos perros temen a algunos que respetan algunos mamíferos.

Las reglas de inferencia de RC y RC†, así, son las mismas de R y R† más las siguientes:

Tabla 10: Reglas de RC y RC†

∀(p, q) ⊢∀(∀(q, r), ∀(p, r))

∀(p, q) ⊢∀(∃(p, r), ∃(q, r))

∃(p, q) ⊢∀(∀(p, r), ∃(q, r))

Los siguientes sistemas en la jerarquía, RC(tr) y RC(tr)†, resultan de añadir un conjunto de frases adjetivas comparativas a los sistemas previos, RC y RC†. Las reglas de inferencia son, por tanto, las reglas de RC y RC† más las siguientes reglas:

Tabla 11: Reglas de RC(tr) y RC(tr)†

∀(p, ∃(q, r)) ⊢∀(∃(p, r), ∃(q, r))

∀(p, ∀(q, r)) ⊢∀(∃(p, r), ∀(q, r))

∃(p, ∀(q, r)) ⊢∀(∀(p, r), ∀(q, r))

∃(p, ∃(q, r)) ⊢∀(∀(p, r), ∃(q, r))

Un ejemplo de inferencia (válida) con frases adjetivas comparativas es el siguiente, donde la frase adjetiva comparativa es la expresión es más alto que:

Tabla 12: Ejemplo de inferencia en RC(tr) y RC(tr)†

	Enunciado
1.	Toda jirafa es más alta que todo ñu.
2.	Algún ñu es más alto que cualquier león.
3.	Algún león es más alto que alguna zebra.
⊢	Toda jirafa es más alta que alguna zebra.

Los siguientes sistemas, RC(tr,opp) y RC(tr,opp)†, resultan de añadir un conjunto de frases adjetivas comparativas opuestas a los sistemas RC(tr) y RC(tr)†. Las reglas de inferencia RC(tr,opp) y RC(tr,opp)† son las reglas de RC(tr) y RC(tr)† más las siguientes reglas, donde el superíndice “-1” indica la presencia de una frase adjetiva comparativa opuesta:

Tabla 13: Reglas de RC(tr,opp) y RC(tr,opp)†

∀(p, ∀(q, t)) ⊢∀(q, ∀(p, t−1))	∃(p, ∀(q, t)) ⊢∀(q, ∃(p, t−1))		∀(p, ∃(q, r−1)) ⊢∀(∀(q, r), ∀(p, r))
∃(∃(p, r−1), ∃(q, r)) ⊢∃(p, ∃(q, r))	∃(∀(p, r), ∀(q, r−1)) ⊢∀(p, ∀(q, r−1))		∃(∀(p, r), ∃(q, r−1)) ⊢∃(q, ∀(p, r−1))
∀(p, ∃(q, r)) ∀(∃(p, r−1), ∃(n, r)) ⊢∀(p, ∃(n, r))		∀(p, ∃(q, r)) ∀(∃(p, r−1), ∀(n, r)) ⊢∀(p, ∀(n, r))

Un ejemplo de inferencia (válida) en este sistema es la siguiente, donde ser más grande que y ser más pequeño que son frases adjetivas comparativas opuestas:

Tabla 14: Ejemplo de inferencia en RC(tr,opp) y RC(tr,opp)†

	Enunciado
1.	Todo perro es más grande que algún erizo.
2.	Todo lo que es más pequeño que un perro es más grande que algún gato.
⊢	Todo perro es más grande que un gato.

Pues bien, a modo de resumen, en la jerarquía de Moss los sistemas A, S, S†, R, RC, RC(tr) y RC(tr,opp) son sistemas aristotélicos; sin embargo, dada la negación completa de sustantivos, los sistemas R†, RC†, RC†(tr) y RC†(tr,opp) son sistemas que se ubican más allá de la frontera aristotélica. Todos estos sistemas, junto con la lógica de primer orden con dos variables (FO2), se encuentran por debajo del límite de la frontera Church-Turing, es decir, son sistemas decidibles; a diferencia de la lógica de primer orden (FOL). Adicionalmente, por su vocabulario definido con elementos de primer orden, todos los sistemas de la jerarquía se ubican dentro del límite de los sistemas tipo Peano-Frege. Esto contrasta, por ejemplo, con el sistema S≥, que no hemos considerado en este trabajo por cuestiones de espacio, pero que modela cuantificadores intermedios comparativos como “muchos”, “mayoría”, o “la mitad”.

El desarrollo de esta jerarquía ofrece evidencia positiva de que, como argumenta Moss, es posible implementar un proyecto de lógica natural proponiendo sistemas lógicos con una noción modificada de variable y probando su completud para estar dentro de los límites de la decibilidad. Para ilustrar esto, Moss ha elaborado un mapa que nos permite visualizar su jerarquía (Fig. 1): más adelante volveremos a mencionarla.

Figura 1. La jerarquía de Moss (2015)

2.2. Aspectos generales de la lógica de términos de Sommers

Fred Sommers, más cerca de Aristóteles que de Frege, estaba interesado en el razonamiento en lenguaje natural. Este interés resultó en el desarrollo de un sistema lógico-algebraico conocido como Term Functor Logic (TFL) (o también ATL por Algebraic Term Logic) o lógica de términos y functores (Sommers, 1967; Sommers, 1982; Englebretsen, 1987; Englebretsen, 1996; Sommers y Englebretsen, 2000; Englebretsen y Sayward, 2011).

La innovación de TFL es que asume una sintaxis terminística. Esto es de suyo interesante porque implica volver la mirada a las lógicas de términos, las cuales, como hemos mencionado en una nota anterior, a pesar de haber sido duramente criticadas (Carnap, 1930; Russell, 1937/1900; Geach, 1972, 1980), han resurgido con fuerza después de la segunda mitad del siglo XX. Este resurgimiento puso de manifiesto que podemos modelar razonamiento típico de primer orden sin usar elementos lingüísticos de primer orden —como variables individuales o cuantificadores (cfr. Quine, 1971; Noah, 1980; Kuhn, 1983). En este contexto, el proyecto lógico de Sommers tiene un alcance todavía más amplio: que sea posible usar una lógica de términos en lugar de un sistema de primer orden no tiene nada que ver con el hecho sintáctico, por decirlo de algún modo, de que podemos modelar inferencia típica de primer orden sin cuantificadores o variables, sino con la visión más general de que el lenguaje natural es una fuente genuina de una lógica natural (Sommers, 2005).

Así pues, para comenzar con una representación de enunciados (categóricos), TFL ofrece la siguiente gramática:3

• SaP := −S+P = −S−(−P) = −(−P)−S = −(−P)−(+S)

• SeP := −S−P = −S−(+P) = −P−S = −P−(+S)

• SiP := +S+P = +S−(−P) = +P+S = +P−(−S)

• SoP := +S−P = +S−(+P) = +(−P)+S = +(−P)−(−S)

Dada esta representación sintáctica, TFL ofrece una regla de inferencia para la silogística: una conclusión se sigue válidamente de un conjunto de premisas si y sólo si i) la suma de las premisas es algebraicamente igual a la conclusión y ii) el número de conclusiones con cantidad particular (viz., cero o uno) es igual al número de premisas con cantidad particular (Englebretsen, 1996, p. 167). Así, por ejemplo, si consideramos un silogismo válido, digamos un silogismo tipo aaa-1, podemos ver cómo la aplicación de este método produce la conclusión correcta (Tabla 15).

Tabla 15: Una inferencia válida tipo aaa-1

	Enunciado	TFL
1.	Todos los mamíferos son animales.	-M+A
2.	Todos los perros son mamíferos.	-P+M
⊢	Todos los perros son animales.	-P+A

En el ejemplo anterior podemos ver claramente cómo es que funciona esta regla: i) si sumamos las premisas obtenemos la expresión algebraica (−M+A)+(−P+M)=−M+A−P+M=−P+A, de tal modo que la suma de las premisas es algebraicamente igual a la conclusión, y la conclusión es igual a −P+A, en lugar de +A−P, porque ii) el número de conclusiones con cantidad particular (cero en este ejemplo) es igual al número de premisas con cantidad particular (cero en este ejemplo).

Esta aproximación algebraica, además, es lógicamente interesante porque es capaz de representar y modelar inferencias relacionales, singulares y compuestas sin perder su motivación principal, a saber, que una inferencia es un proceso que ocurre entre términos. Así, por ejemplo, los siguientes casos ilustran cómo representar y modelar inferencias con enunciados relacionales (Tabla 16), singulares4 (Tabla 17) o compuestos5 (Tabla 18).

Tabla 16: Una inferencia válida con enunciados relacionales

	Enunciado	TFL
1.	Algunos caballos son más rápidos que algunos perros.	+C1+(+R12+P2)
2.	Los perros son más rápidos que algunos hombres.	-P2+(+R23+H3)
3.	Lo que es más rápido que lo que es más rápido que los hombres, es más rápido que los hombres (i.e. la relación ser más rápido que es transitiva).	-(+R12+(+R23+H3))+(+R13+H3)
⊢	Algunos caballos son más rápidos que algunos hombres.	+C1+(+R13+H3)

Tabla 17: Una inferencia válida con enunciados singulares

	Enunciado	TFL
1.	Todo hombre es mortal.	-M+L
2.	Sócrates es hombre.	+s+M
⊢	Sócrates es mortal.	+s+L

Tabla 18: Una inferencia válida con enunciados compuestos

	Enunciado	TFL
1.	Si eres Sócrates, eres amigo de Platón.	-[s]+[p]
2.	Eres Sócrates.	+[s]
⊢	Eres amigo de Platón.	+[p]

Todos estos ejemplos están diseñados para mostrar que TFL es capaz de modelar un gran rango de inferencias, a saber, aquellas que la lógica de primer orden es capaz de modelar. Sin embargo, en cierto sentido, TFL es más expresiva que la lógica de primer orden. Consideremos, por ejemplo, la siguiente inferencia (Englebretsen, 1996, p.172):

Platón educó a Aristóteles. Luego, Aristóteles fue educado por Platón.

No parece controversial afirmar que la inferencia anterior es válida, después de todo, es imposible que la premisa sea verdadera y que la conclusión sea falsa. Sin embargo, no es claro cómo es que esta inferencia es válida usando la lógica clásica de primer orden. Consideremos, por mor de explicación, la siguiente representación de primer orden:

Epa ⊢ Epa

En el ejemplo original es evidente que la conclusión es semánticamente equivalente a la premisa, y no obstante, la premisa es sintácticamente diferente a la conclusión. Idealmente, esta diferencia sintáctica debería ser preservada, pues aunque reconocemos que la premisa y la conclusión comparten el mismo significado, la voz activa y la voz pasiva no son sintácticamente equivalentes. Ahora bien, frente a una inferencia como esta, lo que hace la lógica de primer orden es evadir la situación al asumir que la diferencia sintáctica es despreciable porque ambos enunciados comparten el mismo contenido proposicional (cfr. Quine, 1970, p.35-36), pero esto nos parece una solución ad hoc: en la inferencia “p y q, por tanto, q y p” las conjunciones “p y q” y “q y p” también comparten el mismo contenido proposicional pero no por ello decimos que la diferencia sintáctica entre la premisa y la conclusión es despreciable. En contraste, TFL es capaz de preservar la equivalencia semántica y representar la diferencia sintáctica de tal manera que TFL nos permite realizar inferencias con transformaciones de voz activa-pasiva (por ejemplo, aplicando Conm y Asoc (para un sumario de las reglas de TFL vide Apéndice B)):

+p1+(+E12+a2) ⊢ +a2+(+E12+p1)

Más todavía, consideremos otra inferencia válida (Englebretsen, 1996, p.173):

Sócrates educó a un educador de Aristóteles. Luego, alguien a quien Sócrates educó, educó a Aristóteles.

Una representación perspicua del razonamiento anterior en lógica de primer orden es la siguiente:

(∃x)(Esx˄Exa) ⊢ (∃x)(Esx˄Exa)

Sin embargo, nuevamente, esta representación no parece ser una transcripción fidedigna porque no permite preservar una sutil pero significativa diferencia entre la premisa y la conclusión, a saber, el cambio asociativo. En contraste, TFL es capaz de llevar a cabo inferencias con cambios asociativos (por ejemplo, aplicando Asoc):

+s1+(+E12+(+E23++a3)) ⊢ +(+s1+E12)+(+E23+a3)

Por último, consideremos otra inferencia válida de sentido común (Englebretsen, 1996, p.174):

Platón educó a Aristóteles con un diálogo. Luego, Platón educó a Aristóteles.

Una posible representación de la inferencia anterior en lógica de primer orden podría ser:

(∃x)(Dx˄Epax) ⊢ Epa

Ahora bien, como las relaciones Exyz y Exy tienen aridad diferente, una inferencia intuitiva como la anterior no es válida prima facie, y por tanto, para que tal inferencia sea válida en la lógica clásica de primer orden necesitamos una justificación extralógica que sea capaz de conectar tales relaciones. En contraste, TFL es capaz de llevar a cabo inferencias con simplificaciones poliádicas: TFL preserva la validez de la inferencia poliádica bajo la suposición de sentido común de que la relación educar es poliádica (por ejemplo, aplicando Asoc y Simp):

+p1+((+E123+a2)+D3) ⊢ +p1+(+E123+a2)

Así pues, como se puede apreciar hasta este punto, el sistema TFL ofrece una peculiar álgebra de términos con capacidades expresivas e inferenciales interesantes relacionadas con el modelado de inferencias en lenguaje natural. En efecto, TFL es capaz de modelar la silogística asertórica (con negación completa), la silogística relacional (con negación completa, verbos transitivos, adjetivos comparativos, transformaciones de voz activa-pasiva, cambios asociativos y simplificaciones poliádicas) y la lógica proposicional.

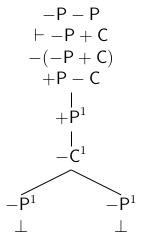
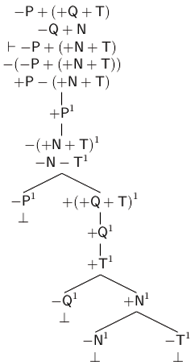
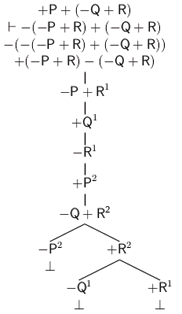
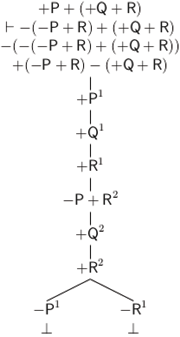
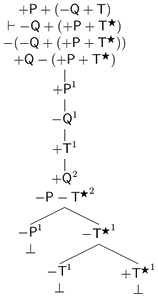
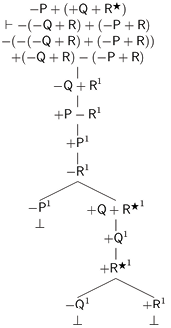
Ahora bien, en otro lugar hemos ofrecido un método de árboles para TFL que preserva sus capacidades expresivas e inferenciales pero que reduce el número de reglas de inferencia y facilita las demostraciones (Castro-Manzano 2018, 2020). Como en este trabajo haremos uso de este método, reproducimos, brevemente, sus nociones básicas. Así, comenzamos por definir, como es usual y siguiendo a (D’Agostino et al, 1999; Priest, 2008), un árbol como un grafo acíclico conectado determinado por nodos y vértices. El nodo superior es la raíz. Los nodos inferiores son puntas. Cualquier camino desde la raíz hasta una punta es una rama. Para probar la validez de una inferencia se construye un árbol que comienza con una única rama cuyos nodos son premisas y la negación de la conclusión: esta es la lista inicial. Entonces se aplican las reglas de expansión que nos permiten extender la lista inicial:

Figura 2. Reglas de expansión

(a)	(b)

En la Figura 2a tenemos la regla para las proposiciones universales tipo a (e) y en la Figura 2b tenemos la regla para las proposiciones particulares tipo i (o). Notemos que al aplicar una regla introducimos un índice i∈{1, 2, 3, ...}. Para las proposiciones universales el índice puede ser cualquier natural; para las proposiciones particulares, tiene que ser un nuevo natural si tales proposiciones no tienen ya un índice asignado. Además, siguiendo las normas de TFL, asumimos las siguientes equivalencias de negación: −(±A) = ∓A, −(±A ± B) = ∓A ∓ B y −(− − A − −A) = +(−A) + (−A). También, como es costumbre, decimos que un árbol es completo si y sólo si toda regla que puede ser aplicada ha sido aplicada. Una rama está cerrada si y sólo si existen términos de la forma ±Ai y ∓Ai en dos de sus nodos; de otro modo está abierta. Una rama cerrada se denota escribiendo ⊥ en su punta; una rama abierta se indica escribiendo ∞ en su punta. Un árbol está cerrado si y sólo si todas sus ramas están cerradas; de otro modo está abierto. Así, como es usual, decimos que A es una consecuencia lógica de un conjunto de términos Γ si y sólo si existe un árbol completo y cerrado cuya lista inicial incluye los términos de Γ y la negación de A.

3. Una traducción terminista de la lógica natural de Moss

A continuación proponemos una traducción de la lógica natural de Moss al sistema TFL de Sommers usando los árboles de TFL. Para alcanzar esta meta seguimos dos pasos: primero, transcribimos las reglas de inferencia de la jerarquía de Moss a expresiones bien formadas de TFL (para llevar a cabo esta transcripción utilizamos letras mayúsculas, como es propio de TFL); posteriormente, mostramos que tales transcripciones resultan en árboles completos y cerrados de TFL.

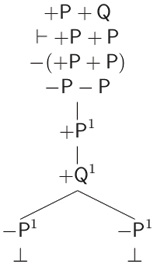
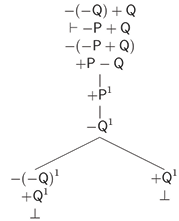
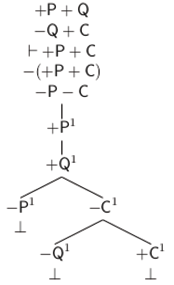
En los Cuadros 19 y 20 presentamos la traducción de los sistemas A, S y S†, y R y R†.

Tabla 19: Sistemas A, S y S†

Sistema			Reglas
S†	S	A	⊢Todo p es p			Todo p es n Todo n es q ⊢Todo p es q
			Algún p es q ⊢Algún q es p		Algún p es q ⊢Algún p es p	Todo q es n Algún p es q ⊢Algún p es n
			Todo q es q ⊢Todo q es p	Todo q es q ⊢Todo p es q		Todo p es q ⊢Todo q es p	Algún p es p ⊢X

Tabla 20: Sistemas R y R†

∃(p, q) ∀(q, c) ⊢∃(p, c)	∀(p, q) ∀(q, c) ⊢∀(p, c)	∀(p, q) ∃(p, c) ⊢∃(q, c)	∀(q, c) ∃(p, c) ⊢∃(p, q)
⊢∀(p, p)	∃(p, c) ⊢∃(p, p)	∀(p, ∀(n, t)) ∃(q, n) ⊢∀(p, ∃(q, t))	∃(p, ∃(q, t)) ∀(q, n) ⊢∃(p, ∃(n, t))
∀(p, p) ⊢∀(p, c)	∃(p, ∃(q, t)) ⊢∃(q, q)	∀(p, ∃(q, t)) ∀(q, n) ⊢∀(p, ∃(n, t))	[φ] … ∃(p, p) ⊢φ

En las Tablas 21 y 22 presentamos la traducción de RC y RC†, y RC(tr) y RC(tr)†.

Tabla 21: Sistemas RC y RC†

∀(p, q) ⊢∀(∀(q, r), ∀(p, r))	∀(p, q) ⊢∀(∃(p, r), ∃(q, r))	∃(p, q) ⊢∀(∀(p, r), ∃(q, r))

Tabla 22: Sistemas RC(tr) y RC(tr)†

∀(p, ∃(q, r)) ⊢∀(∃(p, r), ∃(q, r))	∀(p, ∀(q, r)) ⊢∀(∃(p, r), ∀(q, r))	∃(p, ∀(q, r)) ⊢∀(∀(p, r), ∀(q, r))	∃(p, ∃(q, r)) ⊢∀(∀(p, r), ∃(q, r))

Finalmente, en el Cuadro 23 presentamos la traducción de RC(tr,opp) y RC(tr,opp)†; sin embargo, es preciso hacer un par de aclaraciones previas: para evitar la ambigüedad entre los índices de los árboles y el índice de las frases adjetivas comparativas opuestas, usamos la expresión “★”. Y por último, es notable que algunas de las inferencias del Cuadro 23 son válidas sólo al añadir de manera explícita una proposición que indique la oposición de las frases adjetivas comparativas (i.e. una proposición de la forma -A+A★ para indicar, por ejemplo, que “si X es mayor que Y, Y es menor que X”). Esta adición, no obstante, no representa un problema para TFL, pues dicha adición simplemente significa que la frase comparativa es una premisa implícita.

Tabla 23: Sistemas RC(tr,opp) y RC(tr,opp)†

∀(p, ∀(q, t)) ⊢∀(q, ∀(p, t−1))	∃(p, ∀(q, t)) ⊢∀(q, ∃(p, t−1))	∀(p, ∃(q, r−1)) ⊢∀(∀(q, r), ∀(p, r))	∃(∃(p, r−1), ∃(q, r)) ⊢∃(p, ∃(q, r))
∃(∀(p, r), ∀(q, r−1)) ⊢∀(p, ∀(q, r−1))	∃(∀(p, r), ∃(q, r−1)) ⊢∃(q, ∀(p, r−1))	∀(p, ∃(q, r)) ∀(∃(p, r−1), ∃(n, r)) ⊢∀(p, ∃(n, r))	∀(p, ∃(q, r)) ∀(∃(p, r−1), ∀(n, r)) ⊢∀(p, ∀(n, r))

4. Conclusiones

En este trabajo hemos ofrecido una traducción de la lógica natural de Moss a la lógica de términos de Sommers usando un método de árboles. El resultado de esta traducción muestra que la lógica de términos de Sommers es un sistema alternativo a la lógica natural de Moss que se encuentra más allá de la frontera de los sistemas tipo Peano-Frege, Church-Turing y Aristóteles pero que mantiene el poder expresivo de los sistemas que habitan dentro de los limites de tales fronteras:

i) En efecto, TFL se encuentra más allá de la frontera de los sistemas tipo Peano-Frege por su naturaleza sintáctica terminística; y en la medida en que un subconjunto de TFL se equipara con la jerarquía de Moss, por lo menos un fragmento de TFL se encuentra más de allá de la frontera Church-Turing y de la frontera de los sistemas aristotélicos.

ii) Sin embargo, a pesar de lo anterior, la traducción que hemos presentado muestra que TFL mantiene el poder expresivo de los sistemas equivalentes en la jerarquía de Moss. Más todavía, TFL permite inferencias básicas que no son expresables prima facie en la jerarquía de Moss, como el cambio asociativo o la simplificación poliádica.

Este par de consideraciones nos permite ubicar el lugar del fragmento equivalente de TFL en el mapa de Moss (Figura 3):

Figura 3. El lugar de TFL en la jerarquía de Moss (adaptado de Moss (2015)

Este resultado, así, sugiere que las lógicas de términos, lejos de estar condenadas a ser un episodio superado de la historia de la lógica, pueden ser usadas adecuadamente en la implementación de un proyecto de lógica natural, lo cual es interesante para la filosofía de la lógica y para la teoría de la computación. Para la filosofía de la lógica, porque promueve la revisión de las lógicas de términos (cfr. Veatch, 1970; Sommers, 1982; Englebretsen, 1996; Correia, 2017; Simons, 2020) como herramientas que pueden ser más interesantes y poderosas de lo que originalmente habríamos creído (cfr. Carnap, 1930; Russell, 1937; Geach, 1962; Geach, 1980); y para la teoría de la computación, porque no sólo nos permite reducir el número de reglas de la jerarquía de Moss, sino que, junto con la técnica de árboles, puede ser útil para la programación lógica (cfr. Mozes, 1989; Castro-Manzano y Lozano-Cobos, 2018; Castro-Manzano, 2021).

Por último, nos gustaría añadir que en investigaciones futuras debemos reconsiderar dos tipos de estudios: comparativos y extensivos. Para los primeros sería necesario llevar a cabo una comparación más detallada con los sistemas de demostración algebraica (Carnielli, 2005; Carnielli y Agudelo, 2011), ya que estos sistemas nos permiten reconstruir el análisis booleano de la silogística empleando polinomios además de que pueden extenderse para modelar otros sistemas lógicos. Para los segundos sería necesario extender el modelo de traducción a inferencias en lenguaje natural pero con operadores modales (cfr. Englebretsen, 1998, Malink, 2006), numéricos (cfr. Murphree, 1998) o probabilistas (cfr. Thompson, 1986), además de modelos diagramáticos (cfr. Englebretsen, 1991), y diseños experimentales en psicología (cfr. Keil, 2005; Khemlani y Johnson-Laird, 2012) e inteligencia artificial (cfr. Mozes, 1989).

Referencias

Carnielli, W. A. y Agudelo, J.C. (2011). Polynomial ring calculus for modal logics: A new semantics and proof method for modalities. The Review of Symbolic Logic, 4 (1), 150- 170.

Carnielli, W. A. (2005). Polynomial ring calculus for many-valued logics. 35Th International Symposium on Multiple-Valued Logic (ISMVL’05), 20-25.

Castro-Manzano, J.M. (2018). A Tableaux Method for Term Logic. LANMR 2018, 2264, 1-14.

Castro-Manzano, J.M. (2020). Distribution Tableaux, Distribution Models. Axioms, 9(41).

Castro-Manzano, J.M. (2021). Traditional Logic and Computational Thinking. Philosophies, 6(12).

Castro-Manzano, J.M y Lozano-Cobos, L.I. (2018). TFLPL: Programación con lógica de términos. Research in Computing Science, 147(6), 265-283.

Castro-Manzano, J.M. y Reyes-Cárdenas, P.O. (2018). Term Functor Logic Tableaux. South American Journal of Logic, 4(1), 1-22.

Correia, M. (2017). La lógica aristotélica y sus perspectivas. Pensamiento, 73(275), 5-19.

D’Agostino, M., Gabbay, D.M., Hähnle, R. y Posegga, J. (1999). Handbook of Tableau Methods, Springer.

Englebretsen, G. (1987). The New Syllogistic. Peter Lang.

Englebretsen, G. (1988). Preliminary Notes on a New Modal Syllogistic. Notre Dame J. Formal Logic, 29(3), 381-395.

Englebretsen, G. (1991). Linear Diagrams for Syllogisms (with Relationals). Notre Dame J. Formal Logic, 33(1), 37-69.

Englebretsen, G. (1996). Something to Reckon with: The Logic of Terms. University of Ottawa Press.

Englebretsen, G. y Sayward, C. (2011). Philosophical Logic: An Introduction to Advanced Topics. Bloomsbury Academic.

Geach, P. (1962). Reference and Generality: An Examination of Some Medieval and Modern Theories. Cornell University Press.

Geach, P. (1980). Logic Matters. University of California Press.

Keil, F. (2005). “Exploring Boundary Conditions on the Structure of Knowledge: Some Nonobvious Influences of Philosophy on Psychology”, en Oderberg, D. (ed.), The Old New Logic: Essays on the Philosophy of Fred Sommers, Bradford, 67-84.

Khemlani, S. y Johnson-Laird, P. N. (2012). Theories of the Syllogism: a Meta-Analysis. Psychological Bulletin, 427-457.

Kuhn, S. (1983). An Axiomatization of Predicate Functor Logic. Notre Dame J. Formal Logic, 24(2), 233-241.

Malink, M. (2006). A Reconstruction of Aristotle’s Modal Syllogistic. History and Philosophy of Logic, 27, 95-141.

Moss, L. (2015). “Natural logic”, en Lappin, S. y Fox, C. (eds.), The Handbook of Contemporary Semantic Theory, John Wiley & Sons.

Mozes, E. (1989). A Deductive Database Based on Aristotelian Logic. Journal of Symbolic Computation, 7(5), 487-507.

Murphree, W. (1998). Numerical Term Logic. Notre Dame J. Formal Logic, 39(3), 346-362.

Noah, A. (1980). Predicate-functors and the Limits of Decidability in Logic. Notre Dame J. Formal Logic, 21(4), 701-707.

Noah, A. (2005). “Sommers’s Cancellation Technique and the Method of Resolution”, en Oderberg, D. (ed.), The Old New Logic: Essays on the Philosophy of Fred Sommers, Bradford, 69-182.

Peterson, P. L. (1979). On the Logic of “few”, “many”, and “most”. Notre Dame J. Formal Logic, 20, 155-179.

Priest, G. (2008). An Introduction to Non-Classical Logic: From If to Is. Cambridge University Press.

Quine, W. V. O. (1970). Philosophy of Logic. Englewood Cliffs: Prentice Hall.

Quine, W. V. O. (1971). “Predicate Functor Logic”, en Fenstad, J. E. (ed.), Proceedings of the Second Scandinavian Logic Symposium, North-Holland.

Rini, A.A. (1998). Is There a Modal Syllogistic?. Notre Dame J. Formal Logic, 39(4), 554-572.

Russell, B. (1937/1900). A critical exposition of the philosophy of Leibniz: with an appendix of leading passages, G. Allen & Unwin.

Simons, P. (2020). Term Logic. Axioms, 9(18).

Sommers, F. (1967). “On a Fregean Dogma”, en Lakatos, I. (ed.), Problems in the Philosophy of Mathematics, Elsevier, 47-81.

Sommers, F. (1982). The Logic of Natural Language. Oxford University Press.

Sommers, F. (2005). “Intellectual Autobiography”, en Oderberg, D. (ed.), The Old New Logic: Essays on the Philosophy of Fred Sommers, Bradford, 1-24.

Sommers, F. y Englebretsen, G. (2000). An Invitation to Formal Reasoning: The Logic of Terms. Ashgate.

Thompson, B. (1982). Syllogisms using “few”, “many”, and “most”. Notre Dame J. Formal Logic, 23(1), 75-84.

Thompson, B. (1986). Syllogisms with Statistical Quantifiers. Notre Dame J. Formal Logic, 27(1), 93-103.

Veatch, H. B. (1970). Intentional Logic: A Logic Based on Philosophical Realism. Archon Books.

Apéndice A. Silogística

La silogística asertórica es una lógica de términos que tiene sus orígenes en Primeros analíticos y que estudia la relación de inferencia entre enunciados categóricos. Un enunciado categórico es un enunciado compuesto por dos términos, una cantidad y una cualidad. El sujeto y el predicado del enunciado se llaman términos: el término-esquema S denota el término sujeto y el término-esquema P denota el predicado. La cantidad puede ser universal (Todo) o particular (Algún) y la cualidad puede ser afirmativa (es) o negativa (no es). Estos enunciados se suelen representar mediante una etiqueta: “a” para los enunciados universales afirmativos (i.e. SaP); “e” para los universales negativos (i.e. SeP); “i” para los particulares afirmativos (i.e. SiP); y “o” para los particulares negativos (i.e. SoP). El uso de estas etiquetas nos permite identificar una secuencia de tres enunciados que se conoce como modo: un modo es una secuencia de tres enunciados categóricos ordenados de tal manera que los primeros dos enunciados son premisas y el último enunciados es una conclusión. Un silogismo categórico, entonces, es un modo con tres términos uno de los cuales ocurre en ambas premisas pero no en la conclusión. Este término especial, usualmente denotado con el término-esquema M, funciona como un enlace entre los términos restantes y es conocido como término medio. De acuerdo a la posición del término medio se pueden definir los cuatro arreglos o figuras que codifican los silogismos válidos (Cuadro A1).6

Tabla A1. Modos válidos de la silogística

Figura	1	2	3	4
Modo	aaa	eae	iai	aee
	eae	aee	aii	iai
	aii	eio	oao	eio
	eio	aoo	eio

Apéndice B. Reglas de TFL

• Reglas de inferencia inmediata.

◦ Premisa (P): Cualquier premisa o tautología puede introducirse en una prueba (se excluyen las tautologías que repitan el correspondiente condicional de la inferencia. El correspondiente condicional de una inferencia es un condicional cuyo antecedente es la conjunción de las premisas y cuyo consecuente es la conclusión).

◦ Doble negación (DN): Pares de signos menos unarios pueden ser añadidos o borrados de una fórmula (i.e., --X=X).

◦ Negación externa (NE): Un signo menos unario puede ser distribuido dentro o fuera de cualquier frase (i.e., -(±X±Y)=±X±Y).

◦ Negación interna (NI): Un signo negativo puede ser distribuido dentro o fuera de cualquier término-predicado (i.e., ±X-(±Y)=±X+(±Y)).

◦ Conmutación (Conm): El signo positivo binario es simétrico (i.e., +X+Y=+Y+X).

◦ Asociación (Asoc): El signo positivo binario es asociativo (i.e., +X+(+Y+Z)=+(+X+Y)+Z).

◦ Contraposición (Contra): Los términos sujeto y predicado de una afirmación universal pueden ser negados y pueden intercambiar lugares (i.e., -X+Y=-(-Y)+(-X)).

◦ Distribución de predicado (DP): Un término sujeto universal puede ser distribuido dentro o fuera de un predicado conjuntivo (i.e., -X+(+Y+Z)=+(-X+Y)+(-X+Z)) y un término sujeto particular puede ser distribuido dentro o fuera de un predicado disyuntivo (i.e., +X+ (-(-Y)-(-Z))=--(+X+Y)--(+X+Z)).

◦ Iteración (It): La conjunción de un término consigo mismo es equivalente a dicho término (i.e., +X+X=X).

• Reglas de inferencia mediata

◦ Dictum de omni (DON): Si un término M ocurre universalmente cuantificado en una fórmula y, o bien M ocurre no universalmente cuantificado o su contrario lógico ocurre universalmente cuantificado en otra fórmula, entonces se puede deducir una nueva fórmula que es exactamente como la segunda excepto que M ha sido reemplazada por lo menos una vez por la primera fórmula menos el término M universalmente cuantificado.

◦ Simplificación (Simp): Cualquier conyunto puede ser deducido de una fórmula conjuntiva; de una fórmula cuantificada particularmente con un término sujeto conjuntivo, se puede deducir el término sujeto o un nuevo enunciado justo como el original pero sin uno de los conyuntos del término sujeto (i.e., de +(+X+Y)±Z se deduce cualquiera de las siguientes fórmulas: +X+Y, +X±Z, o +Y±Z), y de una fórmula cuantificada universalmente con un predicado conjuntivo se puede deducir un nuevo enunciado como el original pero sin uno de los conyuntos del término predicado (i.e., de -X±(+Y+Z) se deduce -X±Y o bien -X±Z).

◦ Adición (Ad): Cualesquiera dos fórmulas previas en una secuencia pueden ser unidas para obtener una nueva fórmula, y de cualesquiera dos fórmulas universales afirmativas que compartan un término sujeto común, una nueva fórmula que puede ser deducida es una afirmativa universal que tiene el sujeto de las fórmulas anteriores y tiene la conjunción de los términos predicados de las fórmulas anteriores como el término predicado (i.e., de -X+Y y -X+Z se deduce -X+(+Y+Z)).

---

1 Augustus De Morgan (1860) ya había notado la incapacidad de la lógica de términos aristotélica para lidiar con relaciones, pero fue Russell (1937/1900) quien popularizó la idea de que las limitaciones del programa lógico tradicional, i.e., silogístico (vide Apéndice A), se debían al análisis de los enunciados en clave terminista como triadas de términos sujeto y predicado unidos por una cópula. Posteriormente, Carnap (1930) generalizó esta consideración a toda la lógica tradicional al sostener que la única sintaxis disponible en este tipo de lógica es predicativa. Y si bien estos lı́mites sintácticos pueden parecer menores (ya que producen dificultades para la correcta representación de enunciados singulares, relacionales o compuestos), es la homogeneidad de términos (Geach, 1972; 1980) la dificultad más grave que este tipo de lógicas enfrentan.

2 En este punto, como una revisora nos ha hecho notar, alguien podría observar que la lógica de primer orden trata de estudiar la (in)validez del razonamiento simpliciter, es decir, independientemente de su expresión en un lenguaje natural. Esto nos llevaría a considerar el problema de la representación del razonamiento en lenguaje natural como si fuera un problema externo, extra lógico. Esta observación tiene algo de verdad porque, ciertamente, este no es un problema propio de la lógica de primer orden, sino más bien de su enseñanza y su aplicación en la argumentación o en la filosofía del lenguaje; sin embargo, el hecho de que el problema pueda ser externo no implica que no sea un problema con sus propios méritos, y son justamente problemas externos los que han disparado las discusiones sobre la naturaleza de la lógica, o mejor dicho, las lógicas, y su relación con la argumentación y la filosofía del lenguaje.

3 Aquí seguimos la presentación de (Englebretsen, 1996).

4 Provisto que los términos singulares, como Sócrates, se representan con minúsculas.

5 Dado que los enunciados se pueden representar de la siguiente manera, P:=+[p], Q:=+[q], ¬P:=−[p], P⇒Q:=−[p]+[q], P˄Q:=+[p]+[q] y P˅Q:=−−[p]−−[q], el método se comporta resolución (cfr. Noah, 2005).

6 Sin pérdida de generalidad, omitimos los silogismos que requieren carga existencial.