Daimon. Revista Internacional de Filosofía, nº 91 (2024), pp. 101-119

ISSN: 1130-0507 (papel) y 1989-4651 (electrónico) http://dx.doi.org/10.6018/daimon.379781

Licencia Creative Commons Reconocimiento-NoComercial-SinObraDerivada 3.0 España (texto legal): se pueden copiar, usar, difundir, transmitir y exponer públicamente, siempre que: i) se cite la autoría y la fuente original de su publicación (revista, editorial y URL de la obra); ii) no se usen para fines comerciales; iii) se mencione la existencia y especificaciones de esta licencia de uso (CC BY-NC-ND 3.0 ES)

El carácter idealizado de las leyes de la termodinámica clásica: ¿en qué consiste?

The idealizational aspect of the laws of classic thermodynamics: what does it consist of?

EDGAR EDUARDO ROJAS DURÁN*

---

 

 

Resumen. En la segunda mitad del siglo XX Nowak denunció que las teorías y las leyes científicas tienen un aspecto idealizado que pasaron de largo los filósofos de la ciencia que consideraron como correcto el modelo nomológico deductivo de la explicación científica. En consecuencia, propuso un modelo alternativo de la explicación científica denominado “explicación por concretización gradual” por Hanzel, quien lo retomó, criticó y enmendó a finales del siglo pasado. Ambos autores reconstruyeron varias leyes y teorías científicas empleando su marco conceptual propuesto ignorando la termodinámica clásica o termostática casi por completo. Por esta razón, se pretende aquí aplicar dicho marco conceptual para reconstruir las leyes de la termodinámica clásica y determinar con precisión en qué consiste su aspecto idealizado, así como las implicaciones de este en la interpretación realista de la termodinámica.

Palabras clave: idealización, concretización, explicación científica, leyes científicas, realismo científico.

Abstract. In the second half of the twentieth century Nowak complained that laws and scientific theories have an idealizational aspect that was ignored by most philosophers of science who considered the nomological deductive model of explanation as correct. Therefore, he advanced an alternative model of scientific explanation named “explanation by gradual concretization” by Hanzel, who examined, criticized and improved it at the end of the last century. Both authors reconstructed several scientific theories using their proposed framework disregarding classic thermodynamics almost completely. For this reason, is intended here to deploy such framework in order to reconstruct these laws and to determine precisely of what does consist their idealizational character as well as the implications it has on the realist interpretation of thermodynamics.

Keywords: idealization, concretization, scientific explanation, scientific laws, scientific realism.

Introducción

El objetivo del presente manuscrito es aplicar el modelo de concretización gradual propuesto por Nowak (1972) sobre la teoría de la termodinámica clásica –termostática–, en específico, sus cuatro leyes, para reconocer así el aspecto o carácter idealizado de las leyes que encontramos en su seno. Al reconocer este aspecto se modifica la forma de pensar e interpretar la termodinámica clásica o termostática, pues ya no podría ser pensada o interpretada como refiriendo literal y directamente a sistemas térmicos concretos en situaciones concretas. Esta forma de pensar e interpretar las teorías en general, argüía Nowak, fue la ampliamente compartida por los filósofos de la ciencia pertenecientes al empirismo lógico y la concepción heredada que se desprendía de tomar como correcto el modelo la explicación científica por cobertura legal que pretendía dar cuenta de cómo es que las teorías científicas en general tenían la propiedad de explicar con alto grado de precisión el estado actual de sus objetos de estudio y con el mismo grado de precisión predecir sus futuros estados1.

Este trabajo comienza con la exposición del modelo de la explicación científica por concretización gradual desarrollado por Nowak (1972) y retomado por Hanzel (2008a, 2008b, 2007, 1999) haciendo énfasis en la estructura que este modelo atribuye a las leyes científicas en general. En la segunda sección se continúa con la presentación de la teoría de la termodinámica clásica -termostática- haciendo énfasis en sus cuatro leyes. En la tercera, se aplica el modelo expuesto en la primera sección sobre cada una de las cuatro leyes expuestas en la segunda sección con el fin de mostrar, por un lado, la estructura resultante que obtienen éstas cuando se reconocen las suposiciones idealizantes sobre las que descansan, en breve, su aspecto idealizado y, por el otro, la manera en que se puede dotar de sentido la interpretación realista de éstas mediante el proceso de concretización. Por último, se concluye, acorde al modelo de la explicación científica por concretización gradual, que el aspecto idealizado de las leyes de la termodinámica clásica consiste básicamente en cuatro suposiciones y una quinta en el caso de la tercera ley en su interpretación estadística. Este aspecto idealizado nos obliga a hacer uso de un proceso de concretización para poder interpretarlas de manera realista, es decir, como refiriendo a sistemas térmicos concretos.

I. El modelo de la explicación científica por concretización gradual

Este modelo surge de la denuncia hecha por Nowak de que el problema de la idealización era pasado de largo en ese entonces por las obras más importantes de la filosofía de la ciencia tales como La estructura de la ciencia de Nagel (1961). Este problema, argüía Nowak (1972, 534), aparece en dos ocasiones. La primera es cuando Nagel se pregunta si las teorías científicas refieren al mundo físico y la segunda cuando este mismo autor se pregunta si los teoremas que son verdaderos por vacuidad pueden o no considerarse como leyes científicas. Nowak responde a la primera pregunta afirmativamente, pero agregando que las teorías no aplican directamente sobre fenómenos físicos concretos, sino que requieren de un proceso de concretización para que tenga sentido la afirmación de que refieren al mundo físico. Por otro lado, la segunda interrogante es respondida por Nowak negativamente, pues considera que los enunciados de la forma “Si G(x) y F(x), entonces H(x)” donde F es un término vacío son confirmados de manera indirecta y, en consecuencia, no podrían ser considerados como leyes científicas. Ambas respuestas surgen del reconocimiento del aspecto idealizado de las teorías y de las leyes científicas.

Si reconocemos este aspecto idealizado, la forma de las teorías y de las leyes científicas no corresponderá ya con la forma que atribuyeron los filósofos de la ciencia adheridos al positivismo lógico como Carnap y a la concepción heredada como Hempel. Para este último las explicaciones científicas poseen una estructura lógica donde las leyes científicas juegan un papel imprescindible. En breve, una estructura de cobertura legal. Según él, hay dos tipos o formas de las explicaciones científicas. Una es la nomológica deductiva (Hempel y Oppenheim, 1948). Otra es la inductiva estadística (Hempel, 1958). En el primer tipo un hecho es explicado por una ley científica (enunciado general verdadero) y condiciones iniciales. La ley científica y las condiciones iniciales son pensadas como las premisas que implican deductivamente (explanans) el hecho o evidencia a explicar (explanandum). En breve, en el primer tipo tenemos una estructura de la explicación científica de naturaleza lógica deductiva. En el segundo tipo un hecho es explicado por un enunciado general que expresa probabilidades de que determinados sucesos ocurran (ley estadística) en conjunción con determinadas condiciones iniciales también. Ambos modelos explicativos propuestos por Hempel presentaron dificultades. En lo que concierne al primero, las más destacadas son la de la tesis de la simetría (Scriven, 1962; Bromberger, 1966), así como la de la relevancia causal explicativa (Kyburg, 1965). En lo relativo al segundo, tenemos las dificultades presentadas por Salmon (1967, 1971) relativas a la relevancia estadística explicativa. Cabe señalar que no profundizaremos en estas dificultades, pues no es objetivo del presente manuscrito exponer el modelo de explicación de Hempel, sino solo mencionarlo como un antedecente del que aquí se expone y mostrar que este modelo considera a las leyes científicas como enunciados generales verdaderos. Lo que sí parece pertinente resaltar es que el modelo general de la explicación propuesto por Hempel descansa sobre la concepción sintáctica de la teorías. Esta concepción fue originalmente propuesta por Carnap a lo largo de varias obras en la décadas de los 20s y desarrollada en obras posteriores a los 30s. Esta concepción piensa las teorías como un conjunto de enunciados con cerradura lógica. De esta concepción se desprende lo que mencionamos anteriormente relativo a la forma de pensar las leyes. Esta concepción de las teorías a su vez descansa en el fundacionismo lógico que proponía este mismo autor. El fundacionismo lógico afirmaba que la lógica brindaba los métodos por los que se podía clarificar la estructura, los fundamentos y las aplicaciones de la ciencia. En otras palabras, que el lenguaje científico se reducía en última instancia a lenguaje lógico.

En un intento por superar las críticas al positivismo lógico y la concepción heredada en lo referente a las teorías científicas y, en consecuencia, a las leyes científicas, Nowak argüirá que estas últimas son enunciados universales idealizados, es decir, enunciados producidos como resultado de procesos cognitivos tales como la idealización de los fenómenos físicos concretos que el científico ve en el laboratorio o en las prácticas de campo. Estos tienen la siguiente forma, según Nowak.

N: (x) (Gx&(p1x=d1&..&pk(x)=dk)) Fx = f(H1x,... , Hnx))

Donde N denota un enunciado idealizacional, G un predicado tal que representa la clase de objetos sobre los que la ley aplica, p1, ...., pk, H1, …, Hn y F son términos de funciones definidas sobre el conjunto en el que la variable ‘x’ tiene su rango con valores dentro de los números reales, d1, …, dk ciertos números y f es una función definida en el conjunto de los valores de funciones H1, …, Hn con valores en el conjunto de valores de F. De esta manera, N es un enunciado idealizacional tal que (i) Gx es una suposición realista y p1, …, pn son suposiciones idealizantes (Nowak 1972, 536).

Según Nowak (1972, 536), N hace posible reconstruir leyes científicas populares tales como la de Clayperon. Ésta se expresa mediante la ecuación pv=RT donde p representa la presión de una muestra de gas, v su volumen, R es una constante y T la temperatura de la muestra. Es bien sabido que esta ley es considerada por los mismos científicos como no satisfecha por algún gas encontrado en la naturaleza, sino por gases “ideales” o “perfectos”. Éstos son todos aquellos cuyas partículas pueden considerarse como puntos materiales sin interacciones entre ellos de tal forma que la presión interna de la muestra completa del gas es cero. Estas dos propiedades atribuidas a los gases son el fondo, según Nowak, suposiciones idealizantes las cuales pueden representarse de la siguiente manera:

p1: pw(x) = 0

p2: vw(x) = 0

donde p1 denota la presión interna de la muestra del gas y p2 su volumen. La cantidad de ambas propiedades cuantitativas es igual a cero. Así, la ley de Clayperon es una ley idealizacional cuya forma es la siguiente:

(1) si G(x) y pw(x) = 0 y vw(x) = 0, entonces p(x)v(x) = RT(x)

donde G representa el conjunto de muestras de gases, pw la presión interna de la muestra y vw su volumen.

Una vez formulado (1) se requiere de un proceso de concretización para que tenga sentido la afirmación de que la ley de Clayperon refiere al mundo físico, es decir, a muestras de gas en concreto. Este proceso consiste en la remoción una por una de las suposiciones idealizantes. En este caso las que tienen que ver con la presión y volumen iguales a cero. Al hacer esta remoción se introducen en el consecuente de (1) las correcciones apropiadas. En consecuencia, la concretización de (1) está dada por el siguiente par de enunciados:

(2) si G(x) y p1(x) = d1 y … y pk-1(x) = dk-1 y pk(x) distinto de dk, entonces F(x)=g(H1(x),…,Hn(x),pk(x))

(3) si G(x) y p1(x) = d1 y … y pj(x) = dj y … y pj+1(x) es distinto de dj+1 y …
y pk(x) es distinto de dk, entonces F(x) = h(H1(x),…,Hn(x),Pk(x),…,pj+1(x))

Ambos enunciados pretenden un acercamiento a los hechos concretos introduciendo las correcciones apropiadas que vuelvan las relaciones simples expresadas en (1) cada vez más complejas.

(4) si G(x) y p1(x) se aproximan a d1 y … y pj(x) se aproxima a dj y … y pj+1 es distinto a dj+1 y … y pk(x) es distinto de dk, entonces F(x) se aproxima a h(H1(x), …, Hn(x), pk(x), …, pj+1(x)).

Además de la reconstrucción de leyes científicas en la física, Nowak también reconstruyó leyes científicas en la economía tales como la del valor. Ésta afirma que los precios de las materias primas están conformados tomando en cuenta su valor, es decir, la cantidad de tiempo socialmente indispensable para producirlas. Según, Nowak, esta ley puede ser reformulada de la siguiente manera: (a) “Si x es una materia prima y la diferencia entre la demanda por x y el suministro de x es igual a cero, entonces el precio de x depende de forma lineal del valor de esa materia prima” (Nowak 1980, 3). Y tiene la siguiente forma:

(5) Si C(x) y D(x) – S(x) = 0, entonces P(x) = l(V(x))

Así formulada, arguye Nowak, la ley del valor descansa sobre la suposición de que la demanda y el suministro de toda materia prima está en equilibrio siempre y, en consecuencia, (5) no describe estrictamente hablando el fenómeno social de la creación de precios, pues este fenómeno sucede cuando se presenta una relación de desequilibrio constante entre la demanda y el suministro. Si esto es cierto, entonces para saber la razón por la que Marx la denominó la ley básica de la economía capitalista se requiere una reconstrucción sistemática de ella, según Nowak. Esta reconstrucción consiste en enlistar las suposiciones idealizantes sobre las que descansa. Estas son ocho, a saber: i) la materia prima x es producida en las condiciones de la competencia perfecta, es decir, en un mercado donde no hay monopolios dominantes. ii) La diferencia entre las exportaciones y las importaciones de un sistema económico determinado que produce materia prima es igual a cero. iii) La tasa de la plusvalía característica del capital empleado para producir la materia prima x es idéntica a la tasa promedio de la plusvalía característica del capital comprometido en el sistema económico en cuestión como un todo (ya que el valor de la diferencia de estas magnitudes es igual a cero). iv) La diferencia entre la composición orgánica del capital agricultura y el promedio de la composición orgánica del capital remanente en un sistema económico determinado que produce la materia prima x es igual a cero. v) La ganancia mercantil de la materia prima x es igual a cero. vi) La diferencia entre la composición orgánica del capital en esa rama de producción que resulta ser la materia prima x y el promedio de la composición orgánica del capital en toda la economía en cuestión es igual a cero. vii) La diferencia entre el suministro de la materia prima x y la demanda de ella es igual a cero. viii) La diferencia entre la composición orgánica del capital empleado en la producción de la materia prima x y la composición orgánica promedio en esa rama de producción que resulta ser la materia prima x es igual a cero.

Al formalizar cada una de estas condiciones se obtiene una fórmula que representa la estructura de la ley del valor tomando en cuenta su carácter idealizado, es decir, incluyendo cada una de las condiciones idealizantes sobre las que descansa su formulación. De esta manera, (i) se convierte en p1: PC(x), (ii) en p2: E(x) – I(x) = 0, (iii) en p3:m’(x) – M’(x) = 0, (iv) en p4: ORGA(x) – ORGI(x) = 0, (v) en p5: mer(x) = 0, (vi) en p6: ORG(x) – ORGE(x) = 0, (vii) en p7: D(x) – S(x) = 0 y (viii) en p8: Org(x) – ORG(x) = 0. En adición a todas éstas, Nowak enuncia una más, p0: C(x). Ésta última denota que el universo del discurso de la ley del valor consiste en que x es una materia prima y, en consecuencia, es una condición o suposición de carácter realista en vez de una idealizante.

A partir de la formalización de cada una de las condiciones idealizantes, Nowak llega a la siguiente fórmula que representa la estructura de la ley del valor:

T(8) : C(x) & PC(x) & [E(x) – I(x) = 0] & [m’(x) – M’(x) = 0] & [ORGA(x) – ORGI(x) = 0] & [mer(x) = 0] & [ORG(x) – ORGE(x) = 0] & [D(x) – S(x) = 0] & [Org(x) – ORG(x) = 0] P(x) = l(V(x))

Donde el índice 8 significa que hay 8 condiciones hipotéticas o idealizantes. Esta fórmula a su vez puede abreviarse de la siguiente manera:

T(8): Si p0&p1&...&p8 P(x) = l(V(x))

Estas fórmulas, arguye Nowak (1980, 9) son una mucho mejor aproximación a la ley del valor propuesta por Marx en El Capital que (5). Para llegar a ellas se llevo a cabo el siguiente método: analizar las suposiciones bajo las que descansa dicha ley, hacerlas explicitas, formalizar cada una de ellas e introducirlas en el antecedente del condicional donde la ley en cuestión será el consecuente, en breve, identificar y suponer las ocho condiciones que no son satisfechas de hecho por algun sistema económico. Así, llega Nowak a la conclusión de que la ley del valor es vacía dentro del dominio de los sistemas económicos de la misma manera en que la ley de la inercia de Newton y la de Clayperon también lo son en sus respectivos ámbitos discursivos. La vacuidad de las leyes resalta su carácter idealizado y para eliminar dicho carácter vacuo es menester remover una por una las condiciones idealizantes como se hizo patente con la ley de Clayperon. Sólo así podemos dotar de sentido la afirmación de que las leyes explican y/o predicen fenómenos concretos dentro de sus respectivos dominios de aplicación con alto grado de precisión en virtud de que refieren a ciertos aspectos del mundo físico.

A partir de la reconstrucción de la ley del valor de Marx, Nowak concluye ahora que un enunciado idealizacional tiene la siguiente forma:

T(k) Si G(x) y p1(x)=0 y …y pk-1(x)=0 y pk(x)=0, entonces F(x) = fk(H1(x),…, Hn(x))

Donde G(x) es una suposición realista, mientras que p1(x)=0, …, pk(x)=0 son suposiciones idealizantes (k>0).

Con la finalidad de pasar de las condiciones idealizadas p1(x)=0, …, pk(x)=0 a las condiciones menos idealizadas y, en consecuencia, a las condiciones más próximas a las empíricas, uno debería remover cada una de ellas, por ejemplo, pk(x)=0. Al “removerla” se escribirá la condición pk(x)≠0 en su lugar. Luego, hay que introducir la corrección dentro del consecuente de T(k) de tal manera que se exprese la influencia de la magnitud pk sobre la magnitud F. En consecuencia, obtenemos T(k-1), el enunciado que representa la primera concretización de T(k) con respecto a las funciones g,h. Este está dado por la siguiente fórmula:

T(k-1) G(x) y p1(x)=0 y …y pk-1(x)=0 y pk(x)≠0, entonces F(x) = fk-1(H1(x),…, Hn(x), pk(x))=g[fk(H1(x),…,Hn(x),h(pk(x))]

Donde h es una función que representa el impacto del factor pk sobre la magnitud F, mientras que g expresa el tipo de este impacto, es decir, un fortalecimiento o un debilitamiento de la dependencia fk.

Si seguimos el procedimiento hasta eliminar todas las condiciones idealizantes obtenemos el caso límite de la concretización dada por la siguiente fórmula:

T(0) Si G(x) y p1(x)≠0, y … y pk(x)≠0, entonces F(x) = f0(H1(x),…, Hn(x), pk(x),…,p1(x))=[nf1(H1(x),…,Hn(x),(pk(x),…,p2(x)),m(p1(x))]

En esta fórmula se toma en consideración la influencia que tienen todos los factores p1, ... pn sobre la magnitud F.

Cabe señalar que T(0) ya no es un enunciado idealizacional, pues contiene únicamente condiciones realistas. Por consiguiente, T(0) es denominado un enunciado factual por Nowak (1980, 29). Este tipo de enunciados, arguye Nowak, difícilmente son construidos por los científicos, pues concluyen el proceso de concretización en algún punto anterior asumiendo que la influencia de los factores restantes sobre la magnitud investigada es lo suficientemente “pequeña” y, por tanto, los valores reales de ella son lo “suficientemente próximos” a sus valores teóricos, como lo establece el último enunciado idealizacional.

Hanzel (2008a, 2008b, 2007, 1999) bautizó al método anteriormente expuesto como “el método de la explicación (científica) por concretización gradual”. Además de nombrarlo así, Hanzel (1999) lleva a cabo un análisis minucioso de él que lo lleva a concluir que al emplear este método, Nowak no reconstruyó la ley del valor de una forma tal que se pueda considerar ésta como una definición del valor en sí mismo, pues arguye Hanzel, la reconstrucción de Nowak del consecuente de la ley del valor está básicamente incompleta debido a una falta de comprensión cabal de ésta y la de la plusvalía en tanto Nowak pretendía reducir las formas fenomenológicas de estas leyes a la esencia del valor y la plusvalía.

En consecuencia, Hanzel (1999, 44) arguye que para lograr una reconstrucción completa de estas dos leyes es necesario introducir un concepto distinto al de condiciones de modificación o idealizantes tal que posibilite establecer una relación entre las manifestaciones fenomenológicas del valor y la plusvalía con sus correspondientes esencias, pues el concepto dado por Nowak no permite establer tal vínculo en gran medida por que está enfocado meramente en sus formas fenomenológicas.

Por lo anterior, Hanzel (1999, 50) considera que la fórmula que representa la estrucura de las leyes científicas propuesta por Nowak no es correcta, pues definen las causas mediante sus efectos. En consecuencia, no parece haber dentro del marco dado por Nowak una manera de vincular formas fenomenológicas con esencias tal que desde la esencia se sigan las correspondientes manifestaciones fenomenológicas. En consecuencia, la pretensión de Hanzel es que el modelo originalmente propuesto por Nowak permita discriminar entre el caso donde la ecuación de una ley científica transmite un vínculo ontológico entre la génesis de los efectos y su causa, y el caso donde la ecuación es modificada con el fin epistémico de identificar la causa por el efecto. Para lograr esta distinción Hanzel (1999, 45) introduce una tipología bipartita de leyes de la mano de sus estructuras o fórmulas. Mientras que las leyes de Newton son denominadas “leyes científicas de esencia del tipo idealizacional puro en el k-ésimo grado de idealización” por Hanzel (1999, 46) y están dotadas de la siguiente estructura:

L(k): (x)(Nx&Cmod1-kx = d1-k f1 (Hx) = E(k)(x)

donde N describe el tipo natural para los casos sobre los que aplica la ley formulada, f1 (H) representa una determinada función de la esencia-fundamento-causa, E(k) es el efecto-apariencia en el k-ésimo grado de idealización, Cmod1-k denota una conjunción de 1 a k ceros, constantes o intervalos, Cmod1-k = d1-k es la forma abreviada de la conjunción Cmod1 = d1 &…& Cmodk = dk y representa la conjunción de 1 a k abstracciones a partir de 1 a k condiciones de modificación, las leyes de Marx tales como las de la plusvalía y la del valor son denominadas “leyes científicas del tipo idealizacional inhenrente” por Hanzel (1999, 65) y tienen la siguiente estructura:

L(k): (x)(Nx&Cmod1-kx = d1-k E(k)(x) = f1 (Hx)

donde todas las variables denotan lo mismo, pero el consecuente ha cambiado de tal manera que se representa el hecho de que el efecto-forma fenomenológica E(k) es definida a través de la causa-fundamento-esencia H.

Por último, es importante remarcar que al mismo tiempo que hay una crítica al modelo presentado por Nowak, también hay un reconocimiento de Hanzel (2008b;2007;1999, 84) acerca de sus logros y avances respecto al modelo N-D tales como la inclusión de las condiciones de modificación o idealizantes en el antecedente del enunciado condicional universal, la solución al problema de la explicación de las leyes científicas “teóricas” mediante otras del mismo tipo sin recurrir a estrategias ad hoc, así como la posibilidad de trazar el camino hacia una reconstrucción del vínculo faltante entre las leyes científicas de corte empírico y las de corte inherente.

Cabe mencionar que la última aplicación de este modelo a una teoría científica en concreto se remonta al inicio del presente siglo. Esta aplicación fue sobre la teoría de la selección natural de Darwin (Nowak y Nowakowa, 2000). Sin embargo, esto no quiere decir que no haya trabajos recientes en torno a naturaleza de la idealización científica, por un lado, y el papel que esta juega en la construción de modelos y teorías concretas que encontramos al interior de diversas prácticas científicas, por el otro. Para muestra de lo primero podemos comenzar con el manuscrito de Weisberg (2007). Aquí él distingue tres tipos de idealización: la de modelos múltiples, la galileana, así como la minimalista. Según él, cada una de ellas se emplea con distintos fines y resulta ser afín a determinadas prácticas científicas. El tipo de idealización galileana sería aquel donde Nowak fijó su atención y es en la que se han centrado trabajos como los de McMullin (1985) donde se distinguen tres tipos de técnicas de idealización galileana. Siguiendo la propuesta de Weisberg tenemos los trabajos de De Donato (2012) y de Rohwer y Rice (2013). La primera consiste en presentar un marco conceptual sobre la idealización distinto al de Weisberg con base en el modelo de Fischer-Wright en la biología evolucionista. La segunda consiste en ampliar el marco conceptual provisto por Weisberg añadiendo un cuarto tipo de idealización con base en el juego “halcón-paloma”, un modelo proveniente de la biología evolucionista también. Por otra parte, tenemos una reconstrución en términos estructuralistas del modelo por concretización gradual de Nowak por parte de De Donato (2011), de Balzer y Zoubek (1994), así como de Kuokkanen y Toumivara (1992) a partir de la idea generalizada en filosofía de la ciencia de que la concepción semántica de las teorías es más adecuada y prolífica. Moulines (2007), por ejemplo, arguye que el modelo propuesto originalmente por Nowak debería privilegiar la concepción semántica en vez de la sintáctica por razones metodológicas. Estas consisten basicamente en la relación que guarda la idealización con la construcción y la comparación de modelos. Estos últimos, a partir de la concepción semántica, son generados por las teorías.

II. La termodinámica clásica y sus cuatro leyes

Después de la exposición del método de la explicación (científica) por concretización gradual se pretende aquí aplicar su marco conceptual para determinar la estructura de cada una de las leyes de la termodinámica y así dilucidar su aspecto idealizado. Antes de iniciar con la aplicación del marco conceptual provisto por el modelo de explicación de Nowak sobre la termodinámica clásica o termostática es necesario exponer de manera sucinta el objeto de estudio de la termodinámica y sus cuatro leyes.

Objeto de estudio de la termodinámica

La termodinámica se puede caracterizar como la rama de la física que tiene como objeto de estudio los efectos de los cambios de la temperatura y las transformaciones de la energía en un amplio número de fenómenos (Kestin 1971, 3). Otra forma de hacerlo es afirmando que la termodinámica está por debajo de y dilucida algunos de los conceptos más comunes de la vida diaria tales como la temperatura, el calor y la energía (Atkins 2010, xi).

Así, la termodinámica estudia los sistemas térmicos. Éstos son conjuntos de elementos o partes en los que ocurren procesos de transformación de energía. En principio, casi cualquier cosa puede considerarse como un sistema de esta naturaleza, por ejemplo, un bloque de acero, un motor, un cuerpo humano, etc. La termodinámica se enfoca en las propiedades de estos sistemas, por ejemplo, su temperatura, su calor y su energía interna. Ahora bien, lo que no forma parte de un sistema es denominado alrededores. Aquí es donde se asume se encuentran los observadores de los sistemas térmicos. Éstos son quienes determinan sus estados. La suma de los alrededores y el sistema es equivalente al universo. Por ejemplo, un vaso de precipitados con agua (sistema) en su interior inmerso en agua (alrededores) es igual al universo.

Cabe mencionar que hay una variedad de sistemas. Sus fronteras permiten determinar con precisión cada tipo. Un sistema abierto se define como aquel en el que la materia puede ser añadida o removida, por ejemplo, una bandeja de plástico, madera o metal en cuyo interior se encuentre algún otro objeto material. En este tipo de recipiente podemos agregar o quitar dicho objeto o algunas de sus partes. En contraposición, un sistema cerrado es todo aquel en el que no se puede agregar o quitar materia, por ejemplo, una botella de vidrio o plástico con su tapa bien cerrada y agua en su interior. Luego, por último, un sistema aislado se caracteriza como aquel cuyas fronteras impiden intercambio alguno, por ejemplo, un frasco al vacío con café caliente en su interior.

En general, un sistema posee una variedad de propiedades que son fundamentales para determinar sus posibles estados. Las propiedades que son de interés para la termodinámica son la temperatura (T), la energía (U) y el calor (Q). Cada una de éstas y sus relaciones son introducidas y definidas por las tres primeras leyes. La ley cero introduce y define la propiedad de equilibrio térmico que permite determinar la temperatura (T), mientras que la primera ley hace lo propio con la energía interna (U) y la segunda con la entropía (S).

Para poder determinar en qué consiste el aspecto idealizado de las cuatro leyes de la termodinámica y, en consecuencia, cuál es la estructura que se les atribuye dado el modelo por concretización gradual es menester saber qué afirman con precisión. En consecuencia, en seguida se expone brevemente el contenido de cada una de ellas.

La ley cero de la termodinámica

Dados tres sistemas térmicos A, B y C, si A y B se colocan en contacto térmico2 y no hay alteración en sus estados, entonces determinamos que A y B están en equilibrio térmico3 entre sí, luego si B y C se colocan en contacto térmico y tampoco hay alteración alguna, entonces B y C están en equilibrio térmico también. En consecuencia, si colocásemos ahora en contacto térmico A y C, podemos asegurar que ambos estarán en equilibrio térmico también. (cf. Atkins 2010, 5)

Lo que establece el enunciado mediante el que se expresa la ley cero es que la condición de equilibrio térmico entre los sistemas térmicos es transitiva. Es pertinente resaltar que la ley cero implica la existencia de un criterio para establecer el equilibrio térmico: si las temperaturas de dos sistemas son iguales, entonces ambos sistemas estarán en equilibrio térmico si se ponen en contacto mediante paredes diatérmicas de forma tal que un observador situado fuera de ambos sistemas se percate de que nada cambia en cada uno de ellos (cf. Atkins 2010, 5). Por otra parte, es conveniente remarcar también que la existencia de los aparatos o dispositivos para medir la temperatura (termómetros) tienen como base la ley en cuestión. Un termómetro es llanamente un sistema con una propiedad que podría cambiar si entra en contacto térmico con un sistema cuyas paredes sean diatérmicas. Los termómetros comunes y corrientes hacen uso de la expansión térmica del mercurio o del cambio en las propiedades eléctricas del material que conforma el termómetro.

La primera ley de la termodinámica

Imaginemos un sistema térmico cerrado que es empleado para efectuar trabajo o para liberar un poco de energía en forma de calor. La energía interna de dicho sistema decrecerá. Luego, se deja el sistema aislado de sus alrededores por un tiempo para después volver a él. Hallaremos de forma constante que la capacidad del sistema para efectuar trabajo, su energía interna (U), no vuelve a su valor inicial (anterior al trabajo efectuado o a la liberación de energía en forma de calor). Es decir, la energía interna de un sistema aislado es constante. (cf. Atkins 2010, 21). Lo que equivale a afirmar en última instancia que no hay cambio en la energía interna de un sistema térmico aislado.

La segunda ley de la termodinámica

La segunda ley formulada en términos de la entropía (S) afirma que la cantidad total de entropía del universo aumenta constantemente a través de cualquier cambio espontáneo. Así formulada incorpora los enunciados lógicamente equivalentes de Kelvin y Clausius formulados en términos de calor, trabajo y energía. La formulación de Kelvin afirma que “no es posible efectuar proceso cíclico alguno tal que transforme en trabajo la totalidad del calor que se suministra al sistema desde la fuente”. Por otra parte, la formulación de Clausius sostiene que “la transferencia de calor entre objetos en contacto térmico tiene la dirección que parte del caliente hacia el frío de manera espontánea, es decir, sin efectuar trabajo”. (cf. Atkins 2010, 47-51).

La definición de cambio de entropía ( de un sistema fue dada por Clausius y consiste en la razón entre la energía transferida al sistema térmico como calor (Q) y la temperatura (T) a la que sucedió dicha transferencia. Esto se expresa mediante la siguiente ecuación matemática:

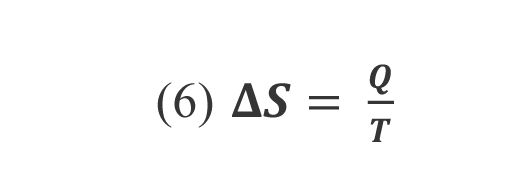
La tercera ley de la termodinámica

Esta ley a diferencia de las tres anteriores no define ninguna propiedad para los sistemas térmicos tales como la energía interna (U) o la entropía (S), sino más bien determina únicamente el comportamiento de la entropía (S) de un sistema cuando su temperatura se aproxima al cero absoluto. En su forma clásica esta ley es expresada mediante la siguiente proposición: “no hay una secuencia finita de procesos cíclicos que pueda lograr exitosamente enfriar (empleando técnicas térmicas convencionales) un cuerpo hasta el cero absoluto”.

La expresión clásica de esta ley es el resultado de los intentos experimentales infructuosos por extraer la totalidad del calor de un objeto conforme su temperatura disminuye casi por completo acercándose al cero absoluto empleando técnicas térmicas convencionales. Éstas son las utilizadas en la fabricación de refrigeradores. Tales intentos no fracasan por el simple hecho de que para la reducción de la temperatura de un objeto se necesite llevar a cabo una cantidad de trabajo cada vez mayor y, por lo tanto, una cantidad de energía en incremento constante, sino porque parece existir un límite en la temperatura que un sistema térmico puede alcanzar cuando está va en decremento constante.

En términos de entropía (S) la tercera ley determina su comportamiento cuando la temperatura de un sistema térmico se aproxima a cero estableciendo que la diferencia de entropía (∆S) desaparece cuando esto sucede. En otras palabras, esta ley establece un límite para la cantidad de entropía de un sistema cuando su temperatura se acerca al cero absoluto. El enunciado que la expresa es el siguiente: la entropía de todos los sistemas se acerca a cero conforme su temperatura se aproxima a cero (cf. Kondepudi 2008, 123). Por último, vale la pena mencionar que hay otra forma de expresar esta ley a partir de su interpretación estadística, a saber: “la entropía de todas las sustancias puras perfectamente cristalinas es cero, cuando su temperatura es cero grados Kelvin”.

III. El aspecto idealizado de las cuatro leyes de la termodinámica

Posterior a una exposición sucinta de las cuatro leyes de la termodinámica en su versión clásica o macroscópica nos enfocamos ahora en la aplicación del marco provisto por Nowak y Hanzel para sacar a la luz su carácter idealizado de la mano de la estructura que explicita cada una de las condiciones idealizantes o de modificación que deben satisfacerse para que las leyes en cuestión sean consideradas como válidas o correctas.

El carácter idealizado de la ley cero

Esta ley puede expresarse mediante la siguiente aseveración: “Si A, B y C son sistemas térmicos, entonces si A está en equilibrio térmico con B y B está en equilibrio térmico con C, entonces A estará en equilibrio térmico con C”. Luego, para determinar su carácter idealizado es necesario sacar a la luz las condiciones idealizantes sobre las que descansa tal formulación. La primera consiste en pensar los sistemas térmicos como perfectamente cerrados y la segunda es que los sistemas x,y,z estén separados entre sí a través de una pared perfectamente diatérmica (una que sólo permita el intercambio de energía). Luego, se hace explícito el universo del discurso de la ley: los sistemas térmicos. Finalmente, se le aplica el cuantificador universal. Así, obtenemos la siguiente fórmula:

L0(2): ∀x,y,z {S(x,y,z)&p1(x,y,z)&p2(x,y,z) [(Exy&Eyz)Exz]}

Donde S describe sistema térmico, p1 la condición idealizante de que los sistemas térmicos x,y,z estén perfectamente cerrados y p2 la condición idealizante de que los sistemas x,y,z estén en contacto entre sí a través de una pared perfectamente diatérmica (una que sólo permita el intercambio de energía en algunas de sus formas como el calor) y E la relación de equilibrio térmico. Por otra parte, el superíndice indica el número de condiciones idealizantes bajo las que la ley cero se cumple y el subíndice hace referencia al número de ley. Así, el carácter idealizado de la ley cero consiste en que aplica para todos aquellos sistemas térmicos perfectamente cerrados en contacto mediante paredes perfectamente diatérmicas, cuando en realidad ningún sistema térmico se puede considerar perfectamente cerrado, así como tampoco hay paredes perfectamente diatérmicas.

Ahora bien, si uno quiere dotar de sentido que L0 refiere a sistemas térmicos concretos y, por lo tanto, tiene contenido fáctico en última instancia habrá que llevar a cabo el proceso contrario: el de concretización. Este consiste en remover4 una por una las condiciones idealizantes hasta aquí explicitadas.

Si removemos la suposición idealizante p1 de que los sistemas x,y,z estén perfectamente cerrados, entonces al colocarlos en contacto mediante una pared perfectamente diatérmica entre ellos no se podría garantizar que no haya intercambio de materia entre ellos y sus alrededores. Así, no podremos determinar que x y y estén en equilibrio térmico, como tampoco que y y z lo estén también y, en consecuencia, tampoco podremos determinar si lo estarán x y z. En consecuencia, hemos obtenido la primera concretización de la ley cero. Ésta se expresaría mediante la siguiente fórmula:

L0(1): ∀x,y,z {S(x,y,z)& ¬p1(x,y,z)&p2(x,y,z) (¬ Exy&¬ Eyz& ¬ Exz)]}

Si ahora quitamos solamente la condición idealizante p2 de que los sistemas x,y,z estén en contacto entre sí a través de una pared perfectamente diatérmica, es decir, una pared que permita solamente intercambio de energía en alguna de sus formas tal como el calor, entonces al colocar en contacto los sistemas x y y no podríamos garantizar que no haya intercambio de materia entre ellos a través de la pared que los pone en contacto entre sí y, por lo tanto, no se podría determinar si se encuentran en equilibrio térmico entre sí. De igual forma, lo mismo pasaría al colocar en contacto los sistemas y y z. En consecuencia, si colocásemos en contacto los sistemas x y z tampoco podremos determinar si están en equilibrio térmico. Así, obtenemos la segunda concretización de la ley cero que se expresaría a través de la siguiente forma:

L0(1): ∀x,y,z {S(x,y,z)& p1(x,y,z) )& ¬p2(x,y,z) [(¬Exy&¬ Eyz) ¬Exz]}

Por último, si removemos simultáneamente p1 y p2, entonces con mucho mayor razón tampoco será el caso que el consecuente se obtenga. De esta manea, obtenemos la tercera concretización de la ley cero que es expresada mediante la fórmula que aparece enseguida:

L0(0): ∀x,y,z {S(x,y,z) )& ¬p1(x,y,z) )& ¬p2(x,y,z) ¬ [(Exy&Eyz) Exz]}

Cada una de las tres formulaciones anteriores pretenden aproximarse a los sistemas térmicos concretos de tal manera que entre menor sea el superíndice mayor será su grado de aproximación. En consecuencia, L0(0) es la forma concretizada de la ley cero que más se aproxime a sistemas térmicos concretos. Esta forma concretizada expresa que para los sistemas térmicos concretos no se satisface estrictamente hablando la transitividad del equilibrio térmico entre dos sistemas hacia un tercero.

Por último, es importante mencionar que esta ley en cuestión no está expresada mediante ecuación matemática alguna. Esto se debe a que esta ley no consiste en una relación entre propiedades cuantitativas de los sistemas térmicos, sino más bien consiste en una relación entre una propiedad no cuantitativa de los sistemas térmicos: la de equilibrio térmico. En consecuencia, resulta de interés la reconstrucción de este tipo de leyes en general mediante la aplicación del marco conceptual provisto por Nowak-Hanzel, es decir, a teorías científicas en las que encontramos leyes no expresadas mediante alguna ecuación tales como la cero de la termodinámica. La reconstrucción aquí elaborada es un intento por aplicar este marco fuera de los ejemplos que ambos autores han abordado y parece correcta a la luz de dicho marco.

El carácter idealizado de la primera ley

Esta ley puede reformularse a través de la siguiente aseveración: “para todo sistema térmico aislado su cambio en la energía interna es igual a cero”. Ahora, para encontrar su carácter idealizado es menester iluminar las condiciones idealizantes bajo las que es válida tal aseveración. La primera y única consiste en pensar los sistemas térmicos como perfectamente aislados, es decir, estar envueltos en paredes perfectamente adiabáticas. Luego, explicitamos el universo del discurso sobre el que aplica dicha ley: los sistemas térmicos. Por último, aplicando el cuantificador universal obtenemos la siguiente fórmula:

L1(1): ∀x[S(x)&p1(x) ΔU(x) = 0]

Donde S describe sistema térmico y p1 la condición idealizante de que el sistema térmico x esté aislado. Por otro lado, al igual que en la estructura anterior, el superíndice es un indicador de la cantidad de condiciones idealizantes que deben cumplirse para que la ley sea válida y el subíndice indica el número de ley de la termodinámica. En consecuencia, se afirma que el carácter idealizado de la ley en cuestión consiste en pensar los sistemas térmicos como aislados, es decir, como envueltos en paredes perfectamente adiabáticas, cuando en realidad no se pueden construir paredes perfectamente adiabáticas5.

De la misma manera que con la ley cero, si uno quiere que tenga sentido la interpretación realista de la primera ley habrá que “concretizar” dicha ley. Esto se logra quitando cada una de las condiciones idealizantes sobre las que descansa.

Si quitamos la única suposición idealizante p1 de que el sistema térmico x está perfectamente aislado, entonces la cantidad de energía interna habrá variado. Esto último equivale a afirmar que la diferencia de energía interna del sistema térmico x es distinta de cero. Así, hemos obtenido la concretización total de la primera ley. Ésta queda expresada por la siguiente fórmula:

L1(0): ∀x[S(x)&¬p1(x) ΔU(x) ≠ 0]

A diferencia de la ley cero donde no encontramos una ecuación matemática del lado del consecuente debido a que no entra en juego alguna propiedad cuantitativa de los sistemas térmicos, en la primera ley sí la hay y la cantidad de la propiedad cuantitativa en cuestión se verá afectada al remover la condición idealizante de que el sistema x esté envuelto en paredes perfectamente adiabáticas. En consecuencia, ahora sí habrá una diferencia en su energía interna.

El aspecto idealizado de la segunda ley

Esta ley puede ser reformulada mediante el siguiente enunciado: “para todo sistema térmico, su cantidad de cambio de entropía es igual a la cantidad de calor suministrado a él entre la temperatura a la que se lleva dicho suministro”. De nueva cuenta, para determinar su aspecto idealizado hay que explicitar las condiciones bajo las que dicha afirmación es válida o correcta. La primera tiene que ver con que el sistema térmico en cuestión esté perfectamente cerrado, mientras que la segunda tiene que ver con que el proceso mediante el que se suministra calor al sistema térmico sea perfectamente reversible, es decir, que el proceso sea uniforme y gradual (sin turbulencias) por completo. Luego, se hace explícito nuevamente el universo del discurso de la ley en cuestión: los sistemas térmicos en general. Por último, agregamos el cuantificador universal a lo anterior para obtener la siguiente estructura:

L2(2): ∀x[S(x)&p1(x)&p2(x) ΔS(x) = Q(x)/T(x)]

Donde S denota un sistema térmico, p1 que el sistema térmico sea cerrado, p2 que el calor suministrado al sistema sea mediante un proceso reversible, Q el calor suministrado al sistema, T la temperatura del sistema. De la misma manera que en los dos casos anteriores, el superíndice indica la cantidad de condiciones idealizantes bajo las que la ley es correcta y el subíndice el número de ley de la termodinámica. Por consiguiente, el aspecto idealizado de la segunda ley consiste en caracterizar los sistemas térmicos en cuestión como perfectamente cerrados y los procesos mediante los que se suministra calor a éstos como perfectamente reversibles, cuando en realidad no hay sistemas perfectamente cerrados ni procesos térmicos perfectamente reversibles.

De igual forma, para concretizar L2 y poder interpretarla como refiriendo a sistemas térmicos concretos quitaremos sus respectivas condiciones idealizantes. Así, si removemos la condición idealizante p1 de que el sistema térmico x esté perfectamente cerrado, entonces la diferencia de entropía del sistema térmico x estará dada de manera aproximada al cociente del calor suministrado al sistema y su temperatura. Esto queda expresado por la fórmula siguiente:

L2(1): ∀x[S(x)& ¬p1&p2(x) ΔS(x) ≈ Q(x)/T(x)]

Si ahora quitamos únicamente la condición idealizante p2 que establece que el calor suministrado al sistema sea a través de un proceso perfectamente reversible, entonces la diferencia de entropía del sistema térmico x estará dada de igual manera aproximada por el mismo cociente. Esto se representa de la siguiente manera:

L2(1): ∀x[S(x)& p1&¬p2(x) ΔS(x) ≈ Q(x)/T(x)]

Por último, si removemos simultáneamente p1 y p2, entonces con mucho mayor razón la diferencia de entropía del sistema en cuestión estará dada de manera aproximada por el cociente entre el calor suministrado al sistema y la temperatura que tenga el sistema. De esta manera, obtenemos la tercera concretización de la ley cero que es expresada mediante la fórmula que aparece enseguida:

L2(0): ∀x[S(x)& ¬p1&¬p2(x) ΔS(x) ≈ Q(x)/T(x)]

Cada una de las formulaciones anteriores pretenden expresar el hecho de que la cantidad de entropía del sistema térmico x estará dada de manera aproximada por el cociente entre las propiedades cuantitativas del calor y la temperatura. Al igual que la ley cero, entre menor sea el superíndice mayor será su grado de aproximación. En consecuencia, L2(0) es la forma concretizada de la ley cero que más se aproxime a sistemas térmicos concretos.

El aspecto idealizado de la tercera ley

En su formulación clásica la tercera ley de la termodinámica parece desprenderse de la consecuencia de la definición de entropía dada por Clausius cuando T=0. Si la temperatura de un sistema térmico es cero, entonces (6) se convierte en una división entre cero y, en consecuencia, la entropía de un sistema térmico cualquiera a esa temperatura quedaría indeterminada. Para determinar con exactitud los posibles valores de la entropía cuando T=0, se puede proceder experimentalmente a buscar dicha temperatura. Al perseguir tal fin mediante técnicas de enfriamiento convencionales, se constató que cada vez que se acercaba uno más al cero se incrementaba cada vez más la cantidad de trabajo para dicho propósito sin alcanzar el cero absoluto. De esta manera, esta ley muy bien no podría considerarse como fundamental6 y, por el otro, descansaría sobre las mismas condiciones idealizantes de la segunda, es decir, la suposición de que hay sistemas térmicos perfectamente cerrados.

Por otra parte, si tomamos en cuenta la segunda formulación estadística de la tercera ley, es decir, en términos de entropía y cristales, ésta podría reformularse mediante el siguiente enunciado: “para toda sustancia pura perfectamente cristalina, si su temperatura es cero, entonces su entropía también lo es”. Así formulada parece evidente su aspecto idealizado: suponer la existencia de sustancias puras perfectamente cristalinas, cuando en realidad los cristales al ser enfriados no alcanzarán un único estado fundamental. Sin embargo, dados los propósitos del presente manuscrito no ahondaremos más en esta posible reconstrucción, pues entonces deberíamos reconstruir las leyes anteriores en términos estadísticos también. Esta tarea es sin duda interesante, pero sería motivo de otra investigación.

Conclusión

Después de haber llevado a cabo el ejercicio de reconstruir las cuatro leyes de la termodinámica mediante el marco propuesto por el modelo de la explicación científica por concretización gradual se puede establecer que su carácter idealizado consiste en suponer la existencia de sistemas completamente cerrados, por un lado, totalmente aislados, por el otro; la existencia de paredes perfectamente diatérmicas, la existencia de procesos reversibles por completo, así como la existencia de sustancias cristalinas puras en el caso de la tercera ley en su interpretación estadística.

Al reconocer este aspecto no podemos pensar que las leyes de la termodinámica clásica brinden una descripción literal de sistemas térmicos concretos. Para que cada una de ellas puedan pensarse así, habrá que remover sus respectivas condiciones idealizantes, es decir, habrá que concretizarlas. De esta manera, en última instancia, podemos dotar de sentido la idea de que dichas leyes explican determinados fenómenos físicos concretos.

Esta tesis va acorde con lo argüido por Nowak acerca de que las teorías y las leyes científicas en general poseen un carácter idealizado que no es capturado por el modelo nomológico deductivo de la explicación científica y que este carácter no nos permitiría afirmar que las teorías científicas a través de sus leyes explican y predicen en virtud de que describen literalmente el mundo físico.

Referencias

Atkins, P. (2010), The laws of Thermodynamics: a very short introduction, Clarendon: Oxford University Press.

Balzer, W., Zoubek, W. (1994), «Structuralist Aspects of Idealization», en Kuokkanen M. (ed.): Idealization VII: Structuralism, Idealization and Approximation. Poznán Studies in the Philosophy of the Sciencies, vol. 42, Amsterdam-Atlanta: Rodopi, pp. 57-79.

Bromberger, S. (1966), «Why Questions», en Colodney, R.G. (ed.): Mind and Cosmos, Pittsburgh: University of Pittsburgh Press, pp. 86-111.

Buchdahl, H. (1966), The concepts of classical thermodynamics, Cambridge: Cambridge University Press.

Callen, H. (1985), Thermodynamics and an introduction to Thermostatics, 2da. Ed., Singapur: Wiley.

De Donato, X. (2011), «Idealization within a Structuralist Perspective», Metatheoria, (139), 65-90.

De Donato, X., Arroyo, A. (2012), «The Structure of Idealization in Biological Theories: The Case of the Wright-Fischer Model», Journal for General Philosophy of Science, (43), 11-27.

Hanzel, I. (1999), «The concept of scientific law in the epistemology of science and epistemology», en Renn J., Gavrolu K., Cohen R. (eds.): Boston Studies in Philosophy of Science, vol. 208, Boston: Springer, pp: 33-84.

Hanzel, I. (2007), «Leszek Nowak on Scientific Laws and Scientific Explanation», en Brzezinski J. (ed.): The Courage of Doing Philosophy. Essays Presented to Leszek Nowak, Amsterdam-New York: Rodopi, pp. 167-178.

Hanzel, I. (2008a), «Idealizations and Concretizations in Laws and Explanation in Physics», Journal for General Philosophy of Science, (39), 273-301.

Hanzel, I. (2008b), «Scientific laws and scientific explanations: a differentiated typology», Organon F, (3), 323-344.

Hempel, C.G., Oppenheim, P. (1948), «Studies in the Logic of Explanation», Philosophy of Sciencie, 15(2), 135-175.

Hempel, C.G. (1958), «The Theoretician’s Dilemma », en Feigl H., Scriven M., Maxwell G., (eds.): Concepts, Theories, and the Mind-Body Problem, Minnesota Studies in the Philosophy of Science, vol. 2, Minneapolis: University of Minnesota Press, pp. 98-169.

Kestin, J. (1971), A course in Statistical Thermodynamics, Nueva York: Academic Press.

Kyburg, H. (1965), «Discussion: Salmon’s Paper», Philosophy of Science, 32(139), 147-151.

Kondepudi, D. (2008), Introduction to Modern Thermodynamics, Nueva York: Wiley.

Kuokkanen, M., Toumivaara, T. (1992), «On the Structure of Idealizations. Explorations in the Poznan School Methodology of Science», en Brezinski J. & Nowak L. (eds.): Idealization III: Approximation and Truth, Poznan Studies in the Philosophy of Sciences and Humanities, vol. 25, Amsterdam, Atlanta, GA: Rodopi, pp. 67-102.

McMullin, E. (1985), «Galilean Idealization», Studies in History and Philosophy of Science, (16), 247-273.

Moulines, U. (2007), «Model construction, idealization and scientifica ontologia», en J. Brezinski et al. (eds.): The Courage of Doing Philosophy: Essays Dedicated to Leszek Nowak, Amsterdam-New York: Rodopi, pp. 257-271.

Nagel, E. (1961), The structure of science: problems in the logic of scientific explanation. Londres: Routledge and Keagan Paul.

Nowak, L. (1972), «Laws of science, theory and measurement», Philosophy of Science, (39), 192-201.

Nowak, L. (1980), «The structure of idealization», en Hintikka, J. (ed.): Synthese Lybrary, vol. 108, Dordrecht: Reidel.

Nowak, L., Nowakowa, I. (2000), «Darwin’s Theory of Natural Selection», en Nowak, L., Nowakowa, I. (eds.): Idealization X: the richness of idealization, Amsterdam: Rodopi, pp. 63-94.

Psillos, S. (1999), How science tracks truth, Londres: Routledge.

Rohwer, S., y Rice, C. (2013), «Hypothetical Pattern Idealization and Explanatory Models», Philosophy of Science, (80), 334-355.

Salmon, W. (1967), Foundations of Scientific Inference. Pittsburgh: University of Pittsburgh Press.

Salmon, W. (1971), «Introduction», en Salmon, W. (ed.): Statical Explanation and Statistical Relevance, Pittsburgh: University of Pittsburgh Press.

Scriven, M. (1959), «Truisms as the Grounds for Historical Explanations», en Gardnier, P. (ed.): Theories of History, Nueva York: The Free Press, pp. 443-475.

Weisberg, M. (2007), «Three Kinds of Idealization», Journal of Philosophy, 104(39), 639-659.

---